基本算法

一、基本电路

名称 符号 名称 符号 名称 符号
电池,1个电池,多个电池 电容器 电解电容器(ANSI)
可变电容器 二极管 齐纳二极管
隧道二极管(Tunnel diode) 发光二极管(LED) 光电二极管
可控硅整流器(Silicon-controlled rectifier) 变容二极管(Varicap) 肖特基二极管
保险丝:IEC(上)与ANSI(中与下) 电感元件 TRS插口
可变电阻(ANSI) 电阻器:ANSI(上)与IEC(下) 开关,单刀/单掷(SPST)
开关,单刀/双掷(SPDT:single port double throw) 开关,双刀/双掷(DPDT) 变压器,右线圈中间有抽头
NPN晶体管 PNP晶体管 n-沟道JFET
p-沟道JFET 场效晶体管 真空管二极管
真空管三极管 真空管五极管 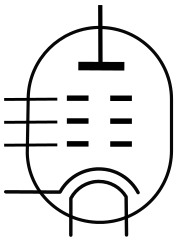真空管四极管
名称 电路图
桥式整流电路
功率放大电路
石英晶体振荡电路
LC振荡电路
RC振荡电路
电压比较电路
差分输入运算放大电路
运算放大电路
选频(带通)放大电路
场效应管放大电路
差分放大电路
串联稳压电源
二极管稳压电路
电路反馈框图
共集电极放大电路(射极跟随器)
分压偏置式共射极放大电路
共射极放大电路
微分和积分电路
信号滤波器
电源滤波器

二、基本运算模拟电路

三、基本函数实现原理

3.1 Taylor级数/展开

在数学中,泰勒级数用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(Sir Brook Taylor)来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数,以苏格兰数学家科林·麦克劳林的名字命名。

拉格朗日在1797年之前,最先提出带有余项的现在形式的泰勒定理。实际应用中,泰勒级数需要截断,只取有限项,可以用泰勒定理估算这种近似的误差。一个函数的有限项的泰勒级数叫做泰勒多项式。一个函数的泰勒级数是其泰勒多项式的极限(如果存在极限)。即使泰勒级数在每点都收敛,函数与其泰勒级数也可能不相等。在开区间(或复平面上的开区间)上,与自身泰勒级数相等的函数称为解析函数。

在数学上,对于一个在实数或复数a邻域上,以实数作为变量或以复数作为变量的函数,并且是无穷可微的函数f(x),它的泰勒级数是以下这种形式的幂级数:

\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}

这里,n!表示n的阶乘,而f^{(n)}(a)\,\!表示函数f在点a处的n阶导数。如果a=0,也可以把这个级数称为麦克劳林级数。

柯西在1823年指出函数\exp \left(-{\frac {1}{x^{2}}}\right)在x=0无法被解析。 如果泰勒级数对于区间(a-r,a+r)中的所有x都收敛并且级数的和等于f(x),那么我们就称函数f(x)为解析形的函数(analytic)。一个函数当且仅当(简单地说,“只有在”)能够被表示为幂级数的形式时,才是解析的函数。通常会用泰勒定理来估计级数的余项,这样就能够确定级数是否收敛于f(x)。上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。

以下三个事实可以说明为什么泰勒级数是十分重要的:

对于一些无穷的可以被微分函数f(x),虽然它们的展开式会收敛,但是并不等于f(x)。例如,分段函数f(x)=\exp \left(-{\frac {1}{x^{2}}}\right),如果x \ne 0并且f(0)=0,则x=0时所有的导数都为零,所以这个f(x)的泰勒级数为零,且其收敛半径为无穷大,不过函数f(x)仅在x=0处为零。但是,在以复数作为变量的函数中这个问题并不存在,因为当z沿虚轴趋于零,\exp \left(-{\frac {1}{z^{2}}}\right)并不趋于零。

如果一个函数在某处引发一个奇点,它就无法被展开为泰勒级数,不过如果变量x是负指数幂的话,我们仍然可以将其展开为一个级数。例如,虽然在x=0的时候,f(x)=\exp \left(-{\frac {1}{x^{2}}}\right)会引发奇点,但仍然能够把这个函数展开为一个洛朗级数。

最近,专家们发现了一个用泰勒级数来求解微分方程的方法——Parker-Sochacki method[1]。用皮卡迭代便可以推导出这个方法。

下面我们给出了几个重要的泰勒级数。当变量x是复数时,这些等式依然成立。

几何级数

{\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+\cdots +x^{n}+\cdots \quad \forall x:\left|x\right|<1

二项式级数

(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}=1+\alpha x+{\frac {\alpha (\alpha -1)}{2!}}x^{2}+\cdots +{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}x^{n}+\cdots \forall x:\left|x\right|<1,\forall \alpha \in \mathbb {C}

其中二项式系数{\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}。

指数函数和自然对数

以e为底数的指数函数的麦克劳林序列是

e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}+\cdots \quad \forall x \, (\text{对所有}X\text{都成立})

以e为底数的自然对数的麦克劳林序列是

\begin{aligned} & \ln(1-x)=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots -{\frac {x^{n}}{n}}-\cdots \quad \forall x\in [-1,1)\,(\text{对于在区间}[-1,1)\text{内所有的}X\text{都成立}) \\ & \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +{\frac {(-1)^{n+1}}{n}}x^{n}+\cdots \quad \forall x\in (-1,1]\,(\text{对于在区间}(-1,1]\text{内所有的}X\text{都成立}) \end{aligned}

三角函数

常用的三角函数可以被展开为以下的麦克劳林序列:

\begin{aligned} \sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&\forall x \\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&\forall x \\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&\forall x:|x|<{\frac {\pi }{2}} \\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&\forall x:|x|<{\frac {\pi }{2}} \\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&\forall x:|x|\leq 1 \\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}+\cdots &&\forall x:|x|\leq 1 \\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&\forall x:|x|\leq 1,\ x\neq \pm i \end{aligned}

在\tan(x)展开式中的Bk是伯努利数。在\sec(x)展开式中的E_k是欧拉数。

双曲函数

\begin{aligned} \sinh x&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)!}}x^{2n+1}\quad \forall x \\ \cosh x&=\sum _{n=0}^{\infty }{\frac {1}{(2n)!}}x^{2n}\quad \forall x \\ \tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}(4^{n}-1)}{(2n)!}}x^{2n-1}\quad \forall x:\left|x\right|<{\frac {\pi }{2}} \\ \sinh ^{-1}x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}\quad \forall x:\left|x\right|<1 \\ \tanh ^{-1}x&=\sum _{n=0}^{\infty }{\frac {1}{2n+1}}x^{2n+1}\quad \forall x:\left|x\right|<1 \end{aligned}

\tanh(x)展开式中的B_k是伯努利数。

朗伯W函数

W_{0}(x)=\sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}x^{n}\quad \forall x:\left|x\right|<{\frac {1}{e}}

多元函数的展开

泰勒级数可以推广到有多个变量的函数:

\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {\partial ^{n_{1}+\cdots +n_{d}}}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}{\frac {f(a_{1},\cdots ,a_{d})}{n_{1}!\cdots n_{d}!}}(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}

3.2 平方根倒数速算法

浮点数的平方根倒数常用于计算正规化向量。3D图形程序需要使用正规化向量来实现光照和投影效果,因此每秒都需做上百万次平方根倒数运算,而在处理坐标转换与光源的专用硬件设备出现前,这些计算都由软件完成,计算速度亦相当之慢;在1990年代这段代码开发出来之时,多数浮点数操作的速度更是远远滞后于整数操作,因而针对正规化向量算法的优化就显得尤为重要。下面陈述计算正规化向量的原理:

要将一个向量标准化,就必须计算其欧几里得范数,以求得向量长度,为此便需对向量的各分量的平方和求平方根;而当求取到其长度,并以之除该向量的每个分量后,所得的新向量就是与原向量同向的单位向量,若以公式表示:

\|\boldsymbol{v}\| = \sqrt{v_1^2+v_2^2+v_3^2}可求得向量v的欧几里得范数,此算法正类如对欧几里得空间的两点求取其欧几里得距离, 而\boldsymbol{\hat{v}} = \boldsymbol{v} / \|\boldsymbol{v}\|求得的就是标准化的向量,若以\boldsymbol{x}代表v_1^2+v_2^2+v_3^2,则有\boldsymbol{\hat{v}} = \boldsymbol{v} / \sqrt{x}, 可见标准化向量时,对向量分量计算平方根倒数实为必需,所以,对平方根倒数计算算法的优化对计算正规化向量也大有裨益。

为了加速图像处理单元计算,《雷神之锤III竞技场》使用了平方根倒数速算法,而后来采用现场可编程逻辑门阵列的顶点着色器也应用了此算法。

下列代码是《雷神之锤III竞技场》源代码中平方根倒数速算法之实例。示例去除了C预处理器的指令,但附上了原有的注释:

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y;                       // evil floating point bit level hacking(对浮点数的邪恶位元hack)
    i  = 0x5f3759df - ( i >> 1 );               // what the fuck?(这他妈的是怎么回事？)
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration (第一次迭代)
//      y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed(第二次迭代,可以删除)

    return y;
}

要理解这段代码,首先需了解浮点数的存储格式。一个浮点数以32个二进制位表示一个有理数,而这32位由其意义分为三段:首先首位为符号位,如若是0则为正数,反之为负数;接下来的8位表示经过偏移处理(这是为了使之能表示-127－128)后的指数;最后23位表示的则是有效数字中除最高位以外的其余数字。将上述结构表示成公式即为\textstyle x=(-1)^{\mathrm {Si} }\cdot (1+m)\cdot 2^{(E-B)},其中\textstyle m表示有效数字的尾数(此处\textstyle 0\leq m<1,偏移量\textstyle B=127,而指数的值\textstyle E-B决定了有效数字(在Lomont和McEniry的论文中称为“尾数”(mantissa))代表的是小数还是整数。以上图为例,将描述带入有\textstyle m=1\times 2^{-2}=0.250),且\textstyle E-B=124-127=-3,则可得其表示的浮点数为\textstyle x=(1+0.250)\cdot 2^{-3}=0.15625。

8位二进制补码示例

符号位
0 1 1 1 1 1 1 1 =127
0 0 0 0 0 0 1 0 =2
0 0 0 0 0 0 0 1 =1
0 0 0 0 0 0 0 0 =0
1 1 1 1 1 1 1 1 =−1
1 1 1 1 1 1 1 0 =−2
1 0 0 0 0 0 0 1 =−127
1 0 0 0 0 0 0 0 =−128

如上所述,一个有符号正整数在二进制补码系统中的表示中首位为0,而后面的各位则用于表示其数值。将浮点数取别名存储为整数时,该整数的数值即为\textstyle I=E\times 2^{23}+M,其中E表示指数,M表示有效数字;若以上图为例,图中样例若作为浮点数看待有\textstyle E=124,M=1\cdot 2^{21},则易知其转化而得的整数型号数值为I=124\times 2^{23} + 2^{21}。由于平方根倒数函数仅能处理正数,因此浮点数的符号位(即如上的Si)必为0,而这就保证了转换所得的有符号整数也必为正数。以上转换就为后面的计算带来了可行性,之后的第一步操作(逻辑右移一位)即是使该数的长整形式被2所除。

S(ign,符号) E(xponent,指数) M(antissa,尾数)
1位 b位 (n-1-b)位
n位

对猜测平方根倒数速算法的最初构想来说,计算首次近似值所使用的常数 0x5f3759df 也是重要的线索。为确定程序员最初选此常数以近似求取平方根倒数的方法,Charles McEniry首先检验了在代码中选择任意常数R所求取出的首次近似值的精度。回想上一节关于整数和浮点数表示的比较:对于同样的32位二进制数字,若为浮点数表示时实际数值为\textstyle x=(1+m_{x})2^{e_{x}},而若为整数表示时实际数值则为\textstyle I_x=E_xL+M_x,其中\textstyle L=2^{n-1-b}。以下等式引入了一些由指数和有效数字导出的新元素:

\begin{aligned} & m_x=\frac{M_x}{L} \\ & e_x=E_x-B,\text{其中}B=2^{b-1}-1 \end{aligned}

再继续看McEniry 2007里的进一步说明:

y=\frac{1}{\sqrt{x}}

对等式的两边取二进制对数(\textstyle \log_2,即函数\textstyle f(n)=2^n的反函数),有

\begin{aligned} & \log_2{(y)}=-\frac{1}{2}\log_2{(x)} \\ & \log_2(1+m_y)+e_y=-\frac{1}{2}\log_2{(1+m_x)}-\frac{1}{2}e_x \end{aligned}

以如上方法,就能将浮点数x和y的相关指数消去,从而将乘方运算化为加法运算。而由于\textstyle \log _{2}{(x)}与\textstyle \log _{2}{(x^{-1/2})}线性相关,因此在\textstyle x与\textstyle y_{0}(即输入值与首次近似值)间就可以线性组合的方式创建方程。在此McEniry再度引入新数\sigma描述\textstyle \log _{2}{(1+x)}与近似值R间的误差:由于\textstyle 0\leq x<1,有\textstyle \log _{2}{(1+x)}\approx {x},则在此可定义\sigma与x的关系为\textstyle \log _{2}{(1+x)}\cong x+\sigma,这一定义就能提供二进制对数的首次精度值(此处0\le\sigma\le\tfrac{1}{3};当R为 0x5f3759df 时,有\textstyle \sigma =0.0450461875791687011756)。由此将\textstyle \log _{2}{(1+x)}=x+\sigma代入上式,有:

m_y+\sigma+e_y=-\frac{1}{2}m_x-\frac{1}{2}\sigma-\frac{1}{2}e_x

参照首段等式代入M_x,E_x,B与L,有:

M_y+(E_y-B)L=-\frac{3}{2}\sigma{L}-\frac{1}{2}M_x-\frac{1}{2}(E_x-B)L

移项整理得:

E_yL+M_y=\frac{3}{2}(B-\sigma)L-\frac{1}{2}(E_xL+M_x)

如上所述,对于以浮点规格存储的正浮点数x,若将其作为长整型表示则示值为\textstyle I_x=E_xL+M_x,由此即可根据x的整数表示导出y(在此\textstyle y=\frac{1}{\sqrt{x}},亦即x的平方根倒数的首次近似值)的整数表示值,也即:

I_y=E_yL+M_y=R-\frac{1}{2}(E_xL+M_x)=R-\frac{1}{2}I_x,\text{其中}R=\frac{3}{2}(B-\sigma)L.

最后导出的等式\textstyle I_{y}=R-{\frac {1}{2}}I_{x}即与上节代码中i=0x5f3759df - (i>>1);一行相契合,由此可见,在平方根倒数速算法中,对浮点数进行一次移位操作与整数减法,就可以可靠地输出一个浮点数的对应近似值。到此为止,McEniry只证明了,在常数R的辅助下,可近似求取浮点数的平方根倒数,但仍未能确定代码中的R值的选取方法。

关于作一次移位与减法操作以使浮点数的指数被-2除的原理,Chris Lomont的论文中亦有个相对简单的解释:以\textstyle 10000=10^{4}为例,将其指数除-2可得\textstyle 10000^{-1/2}=10^{-2}=1/100;而由于浮点表示的指数有进行过偏移处理,所以指数的真实值e应为\textstyle e=E-127,因此可知除法操作的实际结果为\textstyle -e/2+127,这时用R(在此即为“魔术数字”0x5f3759df)减之即可使指数的最低有效数字转入有效数字域,之后重新转换为浮点数时,就能得到相当精确的平方根倒数近似值。在这里对常数R的选取亦有所讲究,若能选取一个好的R值,便可减少对指数进行除法与对有效数字域进行移位时可能产生的错误。基于这一标准,0xbe即是最合适的R值,而0xbe右移一位即可得到0x5f,这恰是魔术数字R的第一个字节。

如上所述,平方根倒数速算法所得的近似值惊人的精确,右图亦展示了以上述代码计算(以平方根倒数速算法计算后再进行一次牛顿法迭代)所得近似值的误差:当输入0.01时,以C语言标准库函数计算可得10.0,而InvSqrt()得值为9.9825822,其间误差为0.017479,相对误差则为0.175%,且当输入更大的数值时,绝对误差不断下降,相对误差也一直控制在一定的范围之内。

在进行了如上的整数操作之后,示例程序再度将被转为长整型的浮点数回转为浮点数(对应x = *(float*)&i;),并对其进行一次浮点运算操作(对应x = x*(1.5f - xhalf*x*x);),这里的浮点运算操作就是对其进行一次牛顿法迭代,若以此例说明:

y=\frac{1}{\sqrt{x}}所求的是y的平方根倒数,以之构造以y为自变量的函数,有f(y)=\frac{1}{y^2}-x=0, 将其代入牛顿法的通用公式y_{n+1} = y_{n} - \frac{f(y_n)}{f'(y_n)}(其中y_n为首次近似值), 有y_{n+1} = \frac{y_{n}(3-xy_n^2)}{2},其中f(y)=\frac{1}{y^2}-x,f'(y)=\frac{-2}{y^3}。

整理有y_{n+1} = \frac{y_{n}(3-xy_n^2)}{2} = y_{n}(1.5-\frac{xy_n^2}{2}),对应的代码即为x = x*(1.5f - xhalf*x*x);。

在以上一节的整数操作产生首次近似值后,程序会将首次近似值作为参数送入函数最后两句进行精化处理,代码中的两次迭代(以一次迭代的输出(对应公式中的y_{n+1})作为二次迭代的输入)正是为了进一步提高结果的精度,但由于雷神之锤III引擎的图形计算中并不需要太高的精度,所以代码中只进行了一次迭代,二次迭代的代码则被注释。

3.3 基本函数实现代码

参考: fdlibm实现

3.3.1 sqrt函数

3.3.2 pow函数

3.3.3 sin函数

/* sin(x): Return sine function of x.
 *
 * kernel function:
 *  __kernel_sin        ... sine function on [-pi/4,pi/4]
 *  __kernel_cos        ... cose function on [-pi/4,pi/4]
 *  __ieee754_rem_pio2  ... argument reduction routine
 *
 * Method.
 *  Let S,C and T denote the sin, cos and tan respectively on  [-PI/4, +PI/4]. Reduce the argument 
 *  x to y1+y2 = x-k*pi/2  in [-pi/4 , +pi/4], and let n = k mod 4.
 *  We have
 *
 *      n         sin(x)  cos(x)    tan(x)
 *     ----------------------------------------------------------
 *      0          S       C         T
 *      1          C      -S        -1/T
 *      2         -S      -C         T
 *      3         -C       S        -1/T
 *     ----------------------------------------------------------
 *
 * Special cases:
 *      Let trig be any of sin, cos, or tan.
 *      trig(+-INF)  is NaN, with signals;
 *      trig(NaN)    is that NaN;
 *
 * Accuracy:
 *   TRIG(x) returns trig(x) nearly rounded 
 */

#ifdef __STDC__
    double sin(double x)
#else
    double sin(x)
    double x;
#endif
{
    double y[2],z=0.0;
    int n, ix;

    /* High word of x. */
    ix = __HI(x);

    /* |x| ~< pi/4 */
    ix &= 0x7fffffff;
    if(ix <= 0x3fe921fb) return __kernel_sin(x,z,0);

    /* sin(Inf or NaN) is NaN */
    else if (ix>=0x7ff00000) return x-x;

    /* argument reduction needed */
    else {
        n = __ieee754_rem_pio2(x,y);
        switch(n&3) {
            case 0: return  __kernel_sin(y[0],y[1],1);
            case 1: return  __kernel_cos(y[0],y[1]);
            case 2: return -__kernel_sin(y[0],y[1],1);
            default:
                return -__kernel_cos(y[0],y[1]);
        }
    }
}

3.3.4 cos函数

3.3.5 log函数

四、排序算法

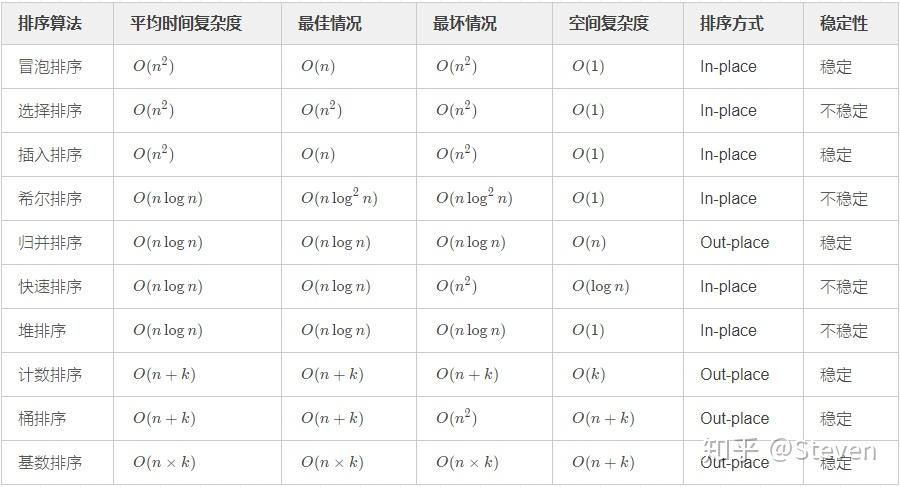
稳定排序:如果a原本在b的前面,且a==b,排序之后a仍然在b的前面,则为稳定排序。

非稳定排序:如果a原本在b的前面,且a==b,排序之后a可能不在b的前面,则为非稳定排序。

原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。

非原地排序:需要利用额外的数组来辅助排序。

时间复杂度:一个算法执行所消耗的时间。

空间复杂度:运行完一个算法所需的内存大小。

n个数顺序的可能情况一共有n!种,如果把每种情况当做二叉树的一个叶子结点,那么每一次比较判断就相当于在二叉树的分叉处选择一个分支,一次排序就可以看做从根节点到一个叶子结点的路径。根据叶子结点有n!个可以得出二叉树的高度至少为\log_2(n!)+1,也就是说至少存在一种情况使得需要比较\log_2(n!)次。根据Stirling公式(n!\sim \sqrt{2\pi n }(n/e)^n)近似,可以得出基于比较的排序算法时间复杂度下限为O(n\log n)。

4.1 选择排序

过程描述:首先找到数组中最小的那个元素,其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。其次在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种方法我们称之为选择排序。

#include <iostream>
#include <algorithm>

using namespace std;
template<typename T> //整数或浮点数皆可使用
void selection_sort(T arr[],int len ) {
    for (int i = 0; i < len  - 1; i++) {
        int min = i;
        for (int j = i + 1; j < len; j++)
            if (arr[j] < arr[min])
                min = j;
        std::swap(arr[i], arr[min]);
    }
}
int main() {
    float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
    int len = (int) sizeof(arrf) / sizeof(*arrf);
    selection_sort(arrf,len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    return 0;
}

平均时间复杂度:O(n^2),空间复杂度:O(1)。

4.2 冒泡排序

冒泡排序是排序算法中较为简单的一种,英文称为Bubble Sort。它遍历所有的数据,每次对相邻元素进行两两比较,如果顺序和预先规定的顺序不一致,则进行位置交换;这样一次遍历会将最大或最小的数据上浮到顶端,之后再重复同样的操作,直到所有的数据有序。

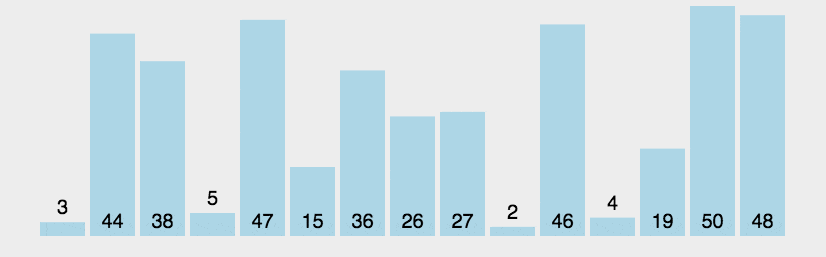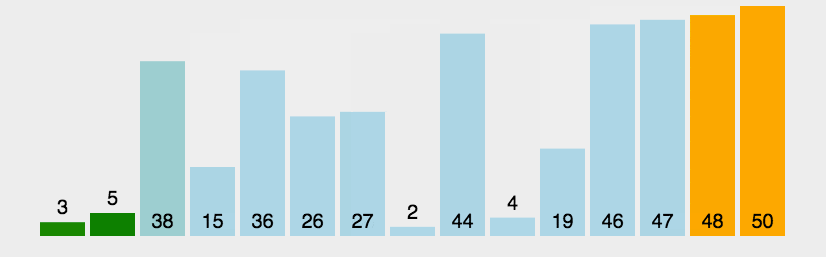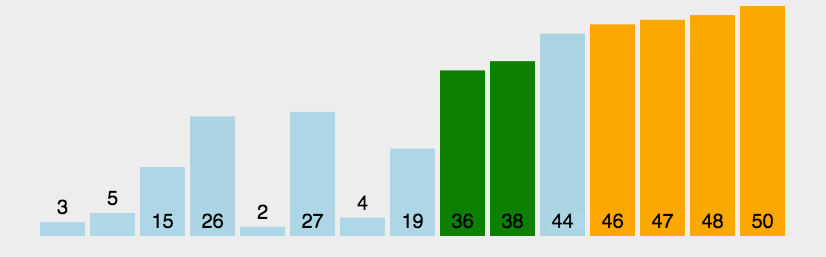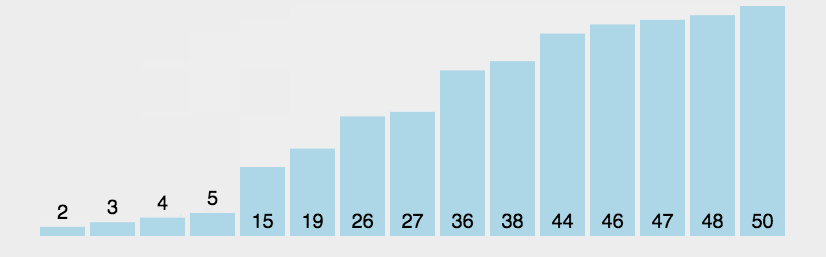
#include <iostream>
#include <algorithm>
using namespace std;
template<typename T> //整数或浮点数皆可使用
void bubble_sort(T arr[], int len) {
    int i, j;
    for (i = 0; i < len - 1; i++){
        for (j = 0; j < len - 1 - i; j++)
            if (arr[j] > arr[j + 1])
                swap(arr[j], arr[j + 1]);
    }
}
int main() {
    int arr[] = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    bubble_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
    len = (int) sizeof(arrf) / sizeof(*arrf);
    bubble_sort(arrf, len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    return 0;
}

平均时间复杂度:O(n^2),空间复杂度:O(1)。

4.3 插入排序

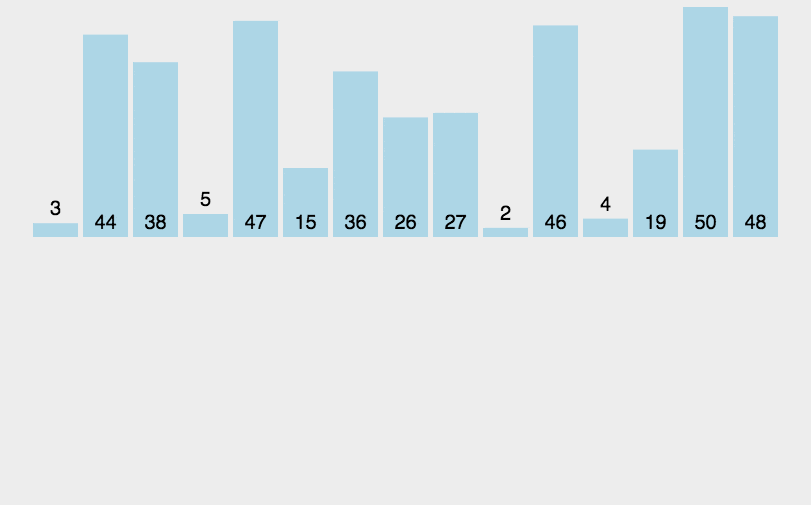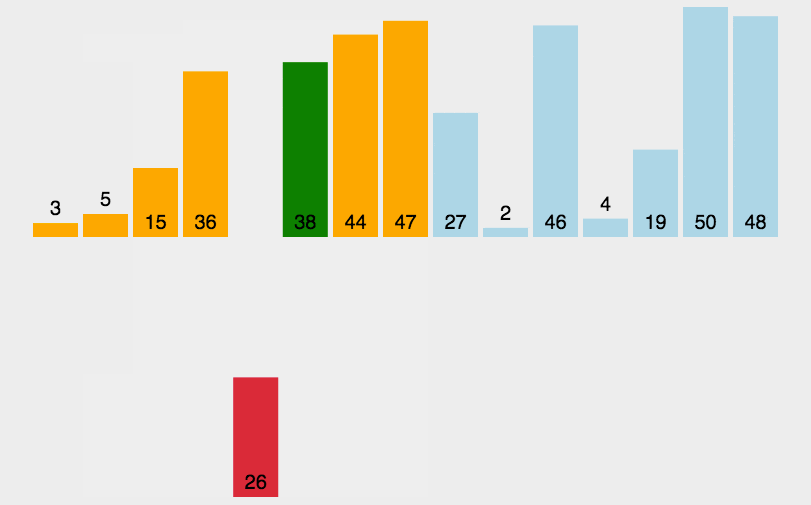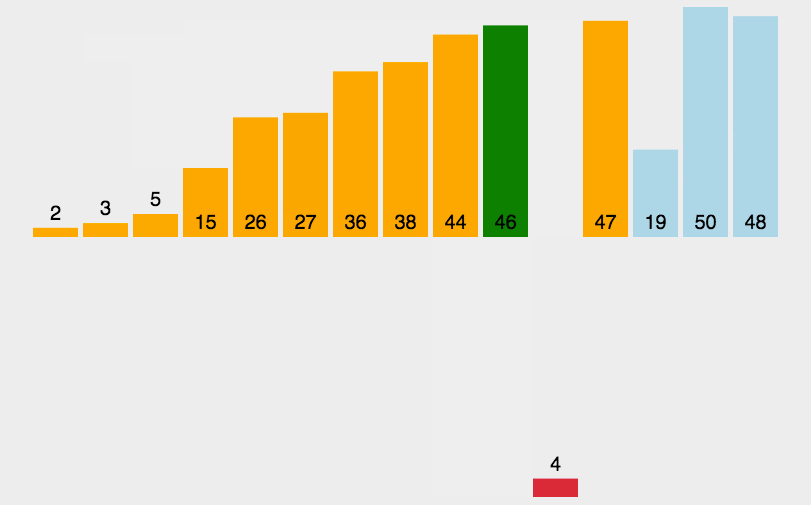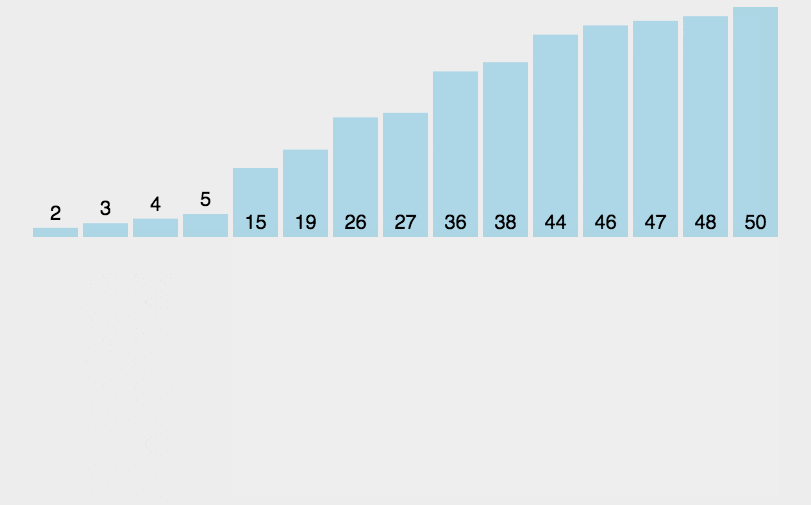
插入排序英文称为Insertion Sort,它通过构建有序序列,对于未排序的数据序列,在已排序序列中从后向前扫描,找到相应的位置并插入,类似打扑克牌时的码牌。插入排序有一种优化的算法,可以进行拆半插入。

基本思路是先将待排序序列的第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列;然后从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置,直到所有数据都完成排序;如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。

#include <iostream>
#include <algorithm>
using namespace std;
template<typename T> //整数或浮点数皆可使用
void insertion_sort(T arr,int len){
    for(int i=1;i<len;i++){
        T key=arr[i];
        int j;
        for(j=i-1;j>=0 && key<arr[j];j--)
            arr[j+1]=arr[j];
        arr[j+1]=key;
    }
}

int main() {
    float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
    int len = (int) sizeof(arrf) / sizeof(*arrf);
    insertion_sort(arrf,len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    return 0;
}

平均时间复杂度:O(n^2),空间复杂度:O(1)。

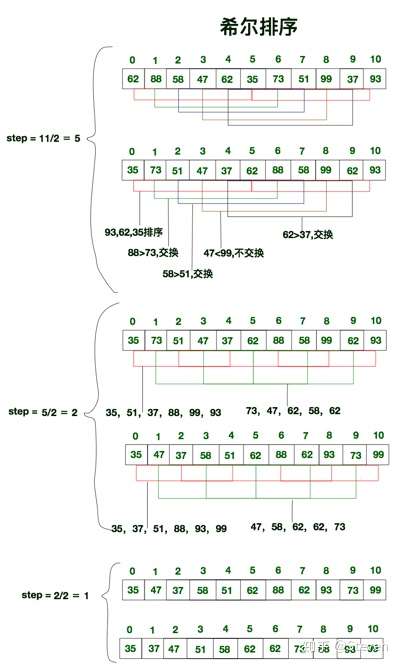
4.4 希尔排序

希尔排序也称递减增量排序,是插入排序的一种改进版本,英文称为Shell Sort,效率虽高,但它是一种不稳定的排序算法。

插入排序在对几乎已经排好序的数据操作时,效果是非常好的;但是插入排序每次只能移动一位数据,因此插入排序效率比较低。

希尔排序在插入排序的基础上进行了改进,它的基本思路是先将整个数据序列分割成若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时,再对全部数据进行依次直接插入排序。

#include <iostream>
#include <algorithm>
using namespace std;
template<typename T>
void shell_sort(T array[], int length) {
    int h = 1;
    while (h < length / 3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        for (int i = h; i < length; i++) {
            for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
                std::swap(array[j], array[j - h]);
            }
        }
        h = h / 3;
    }
}

int main() {
    int arrf[] = { 13，14，94，33，82，25，59，94，65，23，45，27，73，25，39，10 };
    int len = (int) sizeof(arrf) / sizeof(*arrf);
    shell_sort(arrf,len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    return 0;
}

平均时间复杂度: O(n\log n),空间复杂度:O(1)。

4.5 归并排序

归并排序英文称为Merge Sort,归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。它首先将数据样本拆分为两个子数据样本,并分别对它们排序,最后再将两个子数据样本合并在一起;拆分后的两个子数据样本序列,再继续递归的拆分为更小的子数据样本序列,再分别进行排序,直到最后数据序列为1,而不再拆分,此时即完成对数据样本的最终排序。

归并排序严格遵循从左到右或从右到左的顺序合并子数据序列,它不会改变相同数据之间的相对顺序,因此归并排序是一种稳定的排序算法.

作为一种典型的分而治之思想的算法应用,归并排序的实现分为两种方法:自上而下的递归和自下而上的迭代。

#include <iostream>
#include <algorithm>
using namespace std;
template<typename T>
void merge_sort_iteration(T arr[], int len) {//迭代法
    T* a = arr;
    T* b = new T[len];
    for (int seg = 1; seg < len; seg += seg) {
        for (int start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        T* temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        for (int i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    delete[] b;
}
template<typename T>
void merge_sort_recursive_t(T arr[], T reg[], int start, int end) {//递归法
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive_t(arr, reg, start1, end1);
    merge_sort_recursive_t(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
template<typename T>
void merge_sort_recursive(T arr[], const int len) {
    T *reg = new T[len];
    merge_sort_recursive_t(arr, reg, 0, len - 1);
    delete[] reg;
}

int main() {
    float arrf[] = { 17.5, 19.1, 0.6, 1.9, 10.5, 12.4, 3.8, 19.7, 1.5, 25.4, 28.6, 4.4, 23.8, 5.4 };
    int len = (int) sizeof(arrf) / sizeof(*arrf);
    merge_sort_recursive(arrf,len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    merge_sort_iteration(arrf,len);
    for (int i = 0; i < len; i++)
        cout << arrf[i] << ' ';
    return 0;
}

平均时间复杂度:O(n\log n),空间复杂度:O(n)。

4.6 快速排序

快速排序,英文称为Quicksort,又称划分交换排序partition-exchange sort简称快排。

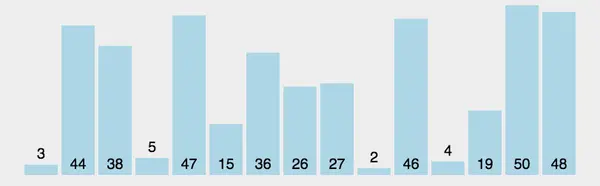
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。首先从数列中挑出一个元素,并将这个元素称为基准,英文pivot。重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。之后在子序列中继续重复这个方法,直到最后整个数据序列排序完成。 在平均状况下,排序n个项目要O(n\log n)次比较。在最坏状况下则需要O(n^2)次比较,但这种状况并不常见。事实上快速排序通常明显比其他算法更快,因为它的内部循环可以在大部分的架构上很有效率地达成。

迭代法:

struct Range {
    int start, end;
    Range(int s = 0, int e = 0) {
        start = s, end = e;
    }
};
template <typename T> //
void quick_sort(T arr[], const int len) {
    if (len <= 0)
        return; //

    Range r[len];
    int p = 0;
    r[p++] = Range(0, len - 1);
    while (p) {
        Range range = r[--p];
        if (range.start >= range.end)
            continue;
        T mid = arr[range.end];
        int left = range.start, right = range.end - 1;
        while (left < right) {
            while (arr[left] < mid && left < right) left++;
            while (arr[right] >= mid && left < right) right--;
            std::swap(arr[left], arr[right]);
        }
        if (arr[left] >= arr[range.end])
            std::swap(arr[left], arr[range.end]);
        else
            left++;
        r[p++] = Range(range.start, left - 1);
        r[p++] = Range(left + 1, range.end);
    }
}

递归法:

template <typename T>
void quick_sort_recursive(T arr[], int start, int end) {
    if (start >= end)
        return;
    T mid = arr[end];
    int left = start, right = end - 1;
    while (left < right) {
        while (arr[left] < mid && left < right)
            left++;
        while (arr[right] >= mid && left < right)
            right--;
        std::swap(arr[left], arr[right]);
    }
    if (arr[left] >= arr[end])
        std::swap(arr[left], arr[end]);
    else
        left++;
    quick_sort_recursive(arr, start, left - 1);
    quick_sort_recursive(arr, left + 1, end);
}
template <typename T> //
void quick_sort(T arr[], int len) {
    quick_sort_recursive(arr, 0, len - 1);
}

平均时间复杂度:O(n\log n,空间复杂度:O(\log n)。

4.7 堆排序

堆排序,英文称Heapsort,是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序实现分为两种方法:

算法步骤:

#include <iostream>
#include <algorithm>
using namespace std;

void max_heapify(int arr[], int start, int end) {
    // 建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { //子节点指标在范围内才做比较
        if (son + 1 <= end && arr[son] < arr[son + 1]) //比较两个子节点大小,选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出函数
            return;
        else { //否則交换父子内容再继续子节点和孙节点比较
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort(int arr[], int len) {
    // 初始化,i从最后一个父节点开始调整
    for (int i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    // 先將第一个元素和已经排好的元素前一位做交换,再重调整(刚调整的元素之前的元素),直到排序完毕
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    return 0;
}

4.8 计数排序

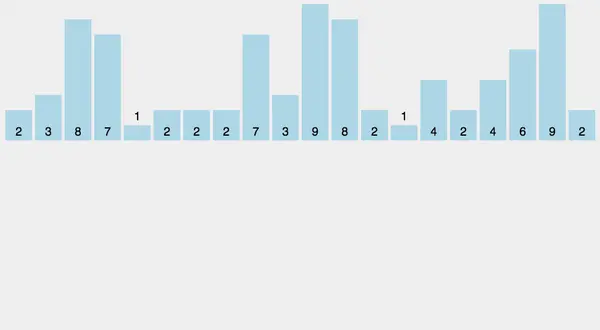
计数排序英文称Counting sort,是一种稳定的线性时间排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。基本的步骤如下:

void  Count_Sort(int* Data, int Len){
    int* Cout = NULL;
    Cout = (int*)malloc(sizeof(int) * Len);
    //初始化记数为0
    for (int i = 0; i < Len; i++) {
        Cout[i] = 0;
    }

    // 记录重复的个数
    for (int i = 0; i < Len; i++){
        Cout[Data[i]] += 1;
    }

    //确定不比该位置大的数据个数。
    for (int i = 1; i < Len; i++){
        Cout[i] += Cout[i - 1];
    }

    int* Sort = NULL;
    Sort = (int*)malloc(sizeof(int) * Len);

    for (int i = 0; i < Len; i++) {
        //将数组反向填充到Sort，每次拿出一个就减一
        Cout[Data[i]] -= 1;
        Sort[Cout[Data[i]]] = Data[i];
    }

    // 排序结束，将排序好的数据复制到原来数组中。
    for (int i = 0; i < Len; ++i){
        Data[i] = Sort[i];
    }

    // 释放申请的空间。
    free(Cout);
    free(Sort);
}

平均时间复杂度:O(n+k),空间复杂度:O(k)。

4.9 桶排序

桶排序也称为箱排序,英文称为Bucket Sort。它是将数组划分到一定数量的有序的桶里,然后再对每个桶中的数据进行排序,最后再将各个桶里的数据有序的合并到一起。

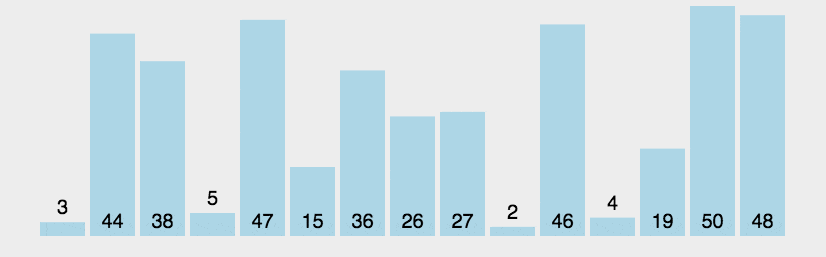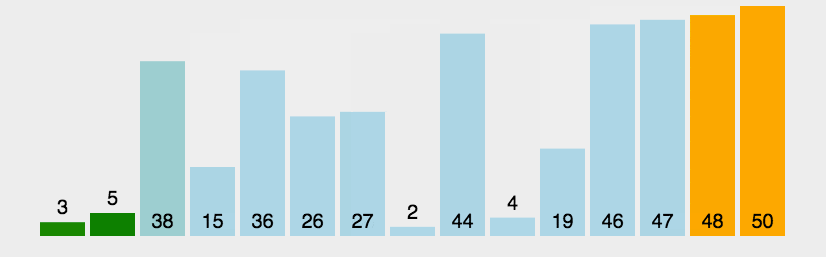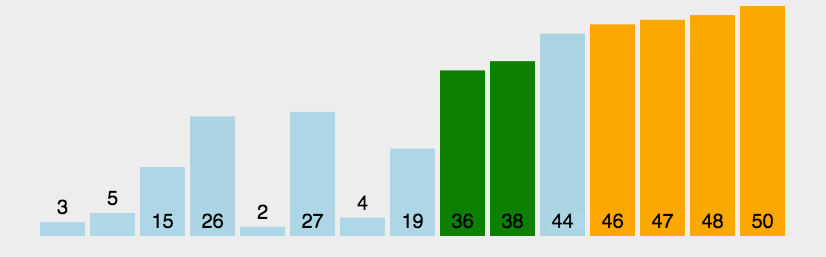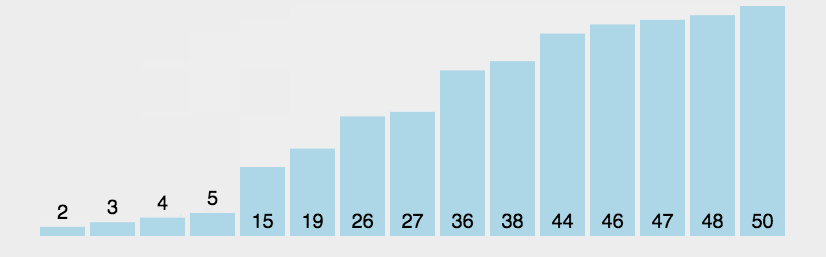
#include <iostream>
#include <vector>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
using namespace std;

struct tNode{
    int tValue;
    tNode *next;

    tNode(int val) {
        this->tValue = val;
        this->next = NULL;
    }
};

bool bucket_sort(int *arrf, const int SIZE){
    tNode **pNode = (tNode **)malloc(sizeof(tNode *) * 512);
    if (NULL == pNode)
        return false;

    memset(pNode, 0, sizeof(tNode *) * 512);

    int shiftNum = 0;
    tNode *p = NULL;
    tNode *pLast = NULL;
    tNode *pNewNode = NULL;

    for (int i = 0; i < SIZE; ++i){
        shiftNum = arrf[i] >> 24;
        p = pNode[shiftNum];

        pNewNode = new tNode(arrf[i]);
        if (NULL == pNewNode)
            return false;

        if (NULL == p){
            pNode[shiftNum] = pNewNode;
        } else if (arrf[i] <= p->tValue) {
            pNode[shiftNum] = pNewNode;
            pNewNode->next = p;
        } else {
            while (NULL != p->next)
            {
                if (arrf[i] > p->next->tValue)
                    p = p->next;
                else
                    break;
            }
            pNewNode->next = p->next;
            p->next = pNewNode;
        }
    }
    for (int i = 0, k = 0; i < 512; i++){
        p = pNode[i];
        while (NULL != p){
            arrf[k++] = p->tValue;
            p = p->next;
        }
    }
    return true;
}
int main(int argc, char **argv){
    int arr[] = { 5,558,772,935,344,487,96,665,302,735,954,308,718,147,185,371,166,849,202,478,874,169,980,125,44,15,279,882,466,974 };

    bucket_sort(arr,30);
    for (int i = 0; i < 30; ++i){
        cout<<arr[i]<<" ";
    }

   cout<<endl;
   return 0;
}

平均时间复杂度:O(n+k),空间复杂度:O(n+k)。

4.10 基数排序

基数排序英文称Radix sort,是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串和特定格式的浮点数,所以基数排序也仅限于整数。它首先将所有待比较数值,统一为同样的数位长度,数位较短的数前面补零。然后从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

int maxbit(int data[], int n) //辅助函数，求数据的最大位数
{
    int maxData = data[0];        ///< 最大数
    // 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
    for (int i = 1; i < n; ++i) {
        if (maxData < data[i])
            maxData = data[i];
    }
    int d = 1;
    int p = 10;
    while (maxData >= p) {
        //p *= 10; // Maybe overflow
        maxData /= 10;
        ++d;
    }
    return d;
}

void radixsort(int data[], int n) //基数排序
{
    int d = maxbit(data, n);
    int *tmp = new int[n];
    int *count = new int[10]; //计数器
    int i, j, k;
    int radix = 1;
    for(i = 1; i <= d; i++) //进行d次排序
    {
        for(j = 0; j < 10; j++)
            count[j] = 0; //每次分配前清空计数器
        for(j = 0; j < n; j++){
            k = (data[j] / radix) % 10; //统计每个桶中的记录数
            count[k]++;
        }
        for(j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
        for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
        {
            k = (data[j] / radix) % 10;
            tmp[count[k] - 1] = data[j];
            count[k]--;
        }
        for(j = 0; j < n; j++) //将临时数组的内容复制到data中
            data[j] = tmp[j];
        radix = radix * 10;
    }
    delete []tmp;
    delete []count;
}

平均时间复杂度:O(n\times k),空间复杂度:O(n+k)。

五、洗牌算法

洗牌(随机)算法有很多应用,例如我们平时用的音乐播放器随机播放,棋牌游戏中的洗牌,扫雷游戏中雷的位置随机等等,都会用到洗牌算法。洗牌可以抽象为:给定一组排列,输出该排列的一个随机组合。

5.1 暴力算法

暴力算法简单的来说就是把每个数放在一个"帽子"里面,每次从"帽子"里面随机摸一个数出来,直到"帽子"为空。下面是具体操作,首先我们把数组array复制一份给数组aux,之后每次随机从aux中取一个数,为了防止数被重复取出,每次取完就把这个数从aux中移除。重置的实现方式很简单,只需把array恢复称最开始的状态就可以了。

这个算法的正确性在于,每次for循环中,任何一个元素都会以等可能的概率被选中。为了证明这一点,我们可以算出来,一个特定的元素e在第k轮被选中的概率为P(e\text{在第}k\text{轮被选中})\cdot P(e\text{在前}k\text{轮不被选中})。假设洗牌的数组有n个元素,这个概率公式如下所示:

\frac{1}{n-k} \cdot \prod_{i=1}^{k} \frac{n-i}{n-i+1}

把这个式子展开一下是这样的:

(\frac{n-1}{n} \cdot \frac{n-2}{n-1} \cdot (\ldots) \cdot \frac{n-k+1}{n-k+2} \cdot \frac{n-k}{n-k+1}) \cdot \frac{1}{n-k}

在k=0的情况下,很显然\frac{1}{n-k} = \frac{1}{n}。对于k>0的情况,前一个式子的分子正好能把下一个式子的分母约去,到最后也只有第一个式子分母还在。因此,不管是哪一轮摸到了哪一个数,概率都是\frac{1}{n},所以这个数组的每个排列组合都是等概率的。

class Solution:
    def __init__(self, nums):
        self.array = nums
        self.original = list(nums)

    def reset(self):
        self.array = self.original
        self.original = list(self.original)
        return self.array

    def shuffle(self):
        aux = list(self.array)

        for idx in range(len(self.array)):
            remove_idx = random.randrange(len(aux))
            self.array[idx] = aux.pop(remove_idx)

        return self.array

复杂度分析:时间复杂度O(n^2),空间复杂度O(n)。

5.2 Fisher-Yates Shuffle算法

最早提出这个洗牌方法的是Ronald A. Fisher和Frank Yates,即Fisher–Yates Shuffle,其基本思想就是从原始数组中随机取一个之前没取过的数字到新的数组中,具体如下:

  1. 初始化原始数组和新数组,原始数组长度为n(已知);
  2. 从还没处理的数组(假如还剩k个)中,随机产生一个[0,k)之间的数字p(假设数组从0开始);
  3. 从剩下的k个数中把第p个数取出;
  4. 重复步骤2和3直到数字全部取完;
  5. 从步骤3取出的数字序列便是一个打乱了的数列

下面证明其随机性,即每个元素被放置在新数组中的第i个位置是1/n(假设数组大小是n)。证明:一个元素m被放入第i个位置的概率P=前i-1个位置选择元素时没有选中m的概率*第i个位置选中m的概率。

#define N 10
#define M 5
void Fisher_Yates_Shuffle(vector<int>& arr,vector<int>& res){
     srand((unsigned)time(NULL));
     int k;
     for (int i=0;i<M;++i) {
        k=rand()%arr.size();
        res.push_back(arr[k]);
        arr.erase(arr.begin()+k);
     }
}

时间复杂度为O(n*n),空间复杂度为O(n).

5.3 Knuth-Durstenfeld Shuffle算法

Knuth和Durstenfeld在Fisher等人的基础上对算法进行了改进,在原始数组上对数字进行交互,省去了额外O(n)的空间。该算法的基本思想和Fisher类似,每次从未处理的数据中随机取出一个数字,然后把该数字放在数组的尾部,即数组尾部存放的是已经处理过的数字。

算法步骤为：

  1. 建立一个数组大小为n的数组arr,分别存放1到n的数值;
  2. 生成一个从0到n-1的随机数x;
  3. 输出arr下标为x的数值,即为第一个随机数;
  4. 将arr的尾元素和下标为x的元素互换;
  5. 同2,生成一个从0到n-2的随机数x;
  6. 输出arr下标为x的数值,为第二个随机数;
  7. 将arr的倒数第二个元素和下标为x的元素互换;
  8. ...
  9. 如上,直到输出m个数为止

该算法是经典洗牌算法。它的proof如下:

void Knuth_Durstenfeld_Shuffle(vector<int>&arr){
    for (int i=arr.size()-1;i>=0;--i) {
        srand((unsigned)time(NULL));
        swap(arr[rand()%(i+1)],arr[i]);
    }
}

时间复杂度为O(n),空间复杂度为O(1),缺点必须知道数组长度n。

原始数组被修改了,这是一个原地打乱顺序的算法,算法时间复杂度也从Fisher算法的O(n^2)提升到了O(n)。由于是从后往前扫描,无法处理不知道长度或动态增长的数组。

5.4 Inside-Out算法

Knuth-Durstenfeld Shuffle是一个内部打乱的算法,算法完成后原始数据被直接打乱,尽管这个方法可以节省空间,但在有些应用中可能需要保留原始数据,所以需要另外开辟一个数组来存储生成的新序列。

Inside-Out算法算法的基本思思是从前向后扫描数据,把位置i的数据随机插入到前i个(包括第i个)位置中(假设为k),这个操作是在新数组中进行,然后把原始数据中位置k的数字替换新数组位置i的数字。其实效果相当于新数组中位置k和位置i的数字进行交互。

如果知道arr的lengh的话,可以改为for循环,由于是从前往后遍历,所以可以应对arr[]数目未知的情况,或者arr[]是一个动态增加的情况。证明如下:

void Inside_Out_Shuffle(const vector<int>&arr,vector<int>& res) {
    res.assign(arr.size(),0);
    copy(arr.begin(),arr.end(),res.begin());
    int k;
    for (int i=0;i<arr.size();++i)
    {
        srand((unsigned)time(NULL));
        k=rand()%(i+1);
        res[i]=res[k];
        res[k]=arr[i];
    }
}

时间复杂度为O(n),空间复杂度为O(n)。

5.5 蓄水池抽样

从N个元素中随机等概率取出k个元素,N长度未知。它能够在O(n)时间内对n个数据进行等概率随机抽取。如果数据集合的量特别大或者还在增长(相当于未知数据集合总量),该算法依然可以等概率抽样。伪代码:

Init : a reservoir with the size k
    for i= k+1 to N
        M=random(1, i);
        if( M < k)
            SWAP the Mth value and ith value
    end for

上述伪代码的意思是:先选中第1到k个元素,作为被选中的元素。然后依次对第k+1至第N个元素做如下操作:每个元素都有k/x的概率被选中，然后等概率的(1/k)替换掉被选中的元素,其中x是元素的序号。

每次都是以k/i的概率来选择证明如下(归纳法)k< i <=N:

  1. 当i=k+1的时候,蓄水池的容量为k,第k+1个元素被选择的概率明显为k/(k+1),此时前k个元素出现在蓄水池的概率为 k/(k+1),很明显结论成立。
  2. 假设当j=i的时候结论成立,此时以k/i的概率来选择第i个元素,前i-1个元素出现在蓄水池的概率都为k/i。证明当j=i+1的情况即需要证明当以k/i+1的概率来选择第i+1个元素的时候,此时任一前i个元素出现在蓄水池的概率都为k/(i+1). i. 前i个元素出现在蓄水池的概率有2部分组成,① 在第i+1次选择前得出现在蓄水池中,② 得保证第i+1次选择的时候不被替换掉 ii. ①由2知道在第i+1次选择前,任一前i个元素出现在蓄水池的概率都为k/i iii. ②. 考虑被替换的概率:首先要被替换得第i+1个元素被选中(不然不用替换了)概率为k/i+1,其次是因为随机替换的池子中k个元素中任意一个,所以不幸被替换的概率是1/k,故 前i个元素(池中元素)中任一被替换的概率=k/(i+1) * 1/k = 1/i+1,则(池中元素中)没有被替换的概率为:1 - 1/(i+1) = i/i+1 iv. 综合①②,通过乘法规则,得到前i个元素出现在蓄水池的概率为 k/i*i/(i+1) = k/i+1
  3. 故证明成立
void Reservoir_Sampling(vector<int>& arr) {
    int k;
    for (int i=M;i<arr.size();++i)
    {
        srand((unsigned)time(NULL));
        k=rand()%(i+1);
        if (k<M)
            swap(arr[k],arr[i]);
    }
}

因此蓄水池抽样因为不需知道n的长度,可用于机器学习的数据集的划分,等概率随机抽样分为测试集和训练集。

5.6 扑克牌洗牌

一堆每张牌都互不一样的牌堆,规定某一种具有随机性的洗牌法。那么在不考虑初始状态的情况下,经过重复进行该洗牌法若干次后,牌堆的每种排列出现的概率都相同或接近相同。问:对某一种确定的洗牌法,若干次是多少次?

目前已经处理解决的洗牌模型及结论如下:

参考文章: Shuffling cards and stopping times

测试洗牌算法的效果:

void testShuffle(char arr[], const int len, void(*shuffle)(char *, const int, char *), const int testTime) {
    int testResult[len][len];
    // testResult[i][j]表示牌arr[i]在第j个位置出现的次数
    std::map<char, int> arrMap; //用于查找牌在原来数组中的位置
    for(int j = 0; j <len; j++) {
        arrMap.insert(map<char, int> :: value_type(arr[j], j));
        memset(testResult[j], 0, len*sizeof(int));
    }

    // 对一副牌洗多次，统计每张牌在每个位置出现的次数
    for(int i = 1; i <= testTime; i++) {
        char arrDest[len];
        shuffle(arr, len, arrDest);
        for(int j = 0; j <len; j++) {
            testResult[arrMap[arrDest[j]]][j] ++;
        }
    }

    for(int i = 0; i < len; i++) {
        printf("%c:", arr[i]);
        for(int j = 0; j < len; j++) {
            printf("%7d",testResult[i][j]);
        }
        printf("\n");
    }
    printf("----------------------------------\n");
}