题目0301:删除无效的括号
题目描述
删除最小数量的无效括号,使得输入的字符串有效,返回所有可能的结果。
说明:输入可能包含了除(和)以外的字符。
示例1:
输入: "()())()"
输出: ["()()()", "(())()"]
示例2:
输入: "(a)())()"
输出: ["(a)()()", "(a())()"]
示例3:
输入: ")("
输出: [""]
解题技巧
- 方法一:回溯
对于这个问题,我们得到了一个由括号组成的表达式,并且表达式中可能有一些错误的括号或额外的括号,导致它无效。只有当每个右括号都有对应的左括号时,由括号组成的表达式才被视为有效,反之亦然。
这意味着,如果我们从左到右查看每个括号,一旦遇到右括号,就应该有一个左括号来匹配它。否则表达式将变为无效。如果左括号的数目大于右括号的数目则表达式也无效。
让我们看看一个无效的表达式和所有可能的有效表达式,这些表达式可以通过删除一些方括号从中形成。我们可以删除哪些括号没有限制。我们只需要使表达式有效。
唯一的条件是,我们应该删除最小的括号数,使一个无效的表达式有效。如果不存在这个条件,我们可以潜在地删除大部分括号。
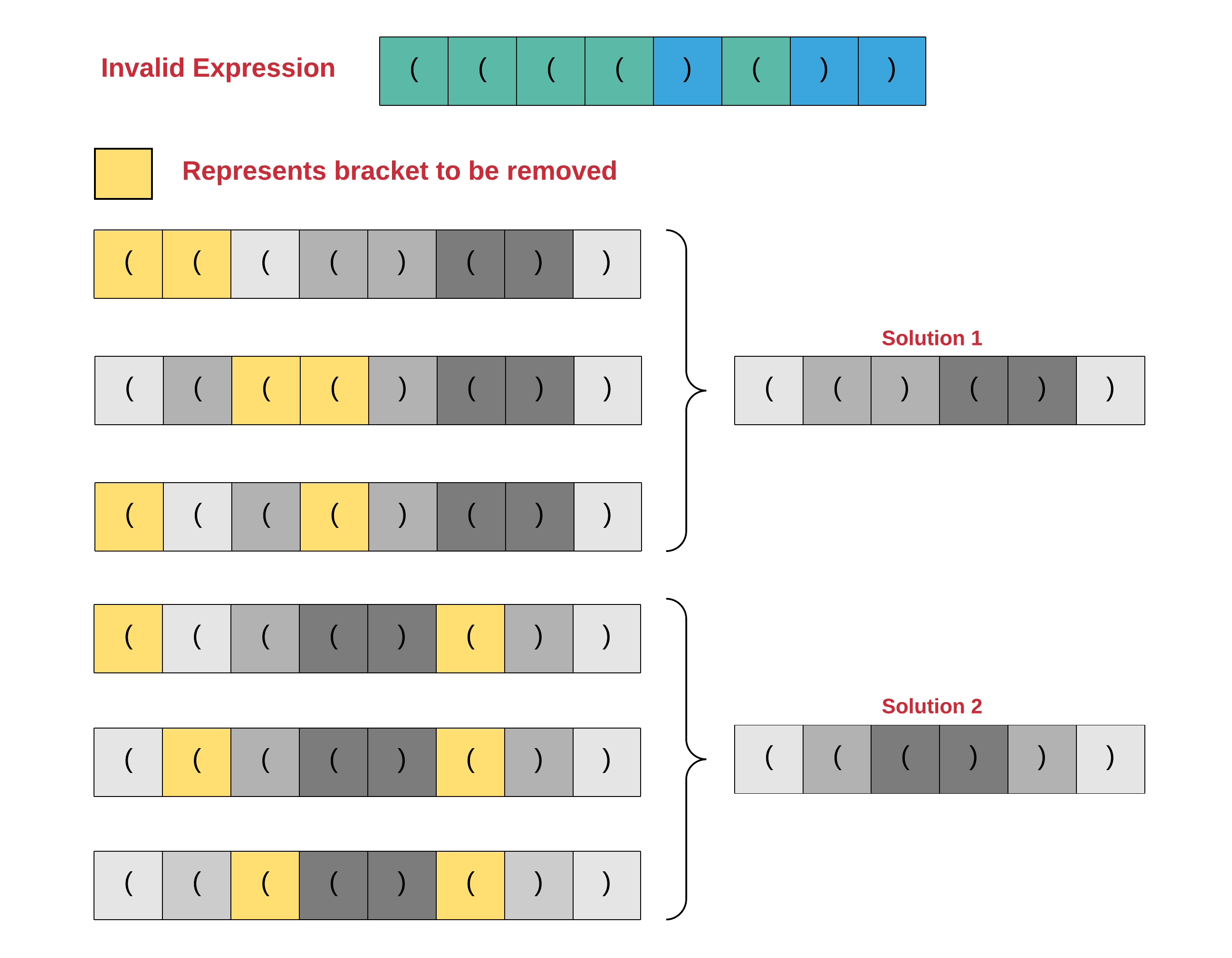
在上图中需要注意的一件重要的事情是,有多种方法可以达到相同的解,也就是说,为了使原始表达式有效,需要删除的括号的最佳数目是k。我们可以删除多组不同的k括号,这些括号最终将给出相同的最终表达式。但是,每个有效表达式只应记录一次。我们必须在解决方案中解决这个问题。请注意,还有其他可能的方法可以达到上面所示的两个有效表达式之一。对于这两个有效表达式,我们只演示了三种方法。
回到我们的问题上来,现在出现的问题是,如何决定要删除哪些括号?因为我们不知道哪一个括号可能被删除,所以我们尝试了所有的选项!
对于每个括号,我们有两个选择:
- 它可以被视为最终表达式的一部分
- 它可以被忽略,也就是说,我们可以从最终表达式中删除它。
这样的问题,我们有多个选择,我们没有战略或指标来贪婪地决定选择哪一个选择,我们尝试了所有的选择,看看哪一个导致了答案。
算法:
- 初始化最终将存储所有有效表达式的数组。
- 从给定序列中最左边的括号开始,然后向右递归
- 递归状态由我们当前在原始表达式中处理的索引定义。让这个索引用字符i来表示。另外,我们有两个不同的变量left_count和right_count,它们表示我们到目前为止添加到表达式中的左括号和右括号的数目。这些是被考虑的括号。
- 如果当前字符,即si既不是右括号也不是左括号,那么我们只需将此字符添加到当前递归的最终解决方案字符串中。
- 但是,如果当前字符是两个方括号中的一个,即S[i] == '(' or S[i] == ')',则我们有两个选项。我们可以通过将此字符标记为无效字符来丢弃它,也可以将此括号视为最终表达式的一部分。
- 当原始表达式中的所有括号都被处理后,我们只需检查expr表示的表达式是否有效,即到目前为止形成的表达式是否有效。我们检查最后一个表达式是否有效的方法是通过查看left_count和right_count的值。表达式必须是有效的left_count == right_count。如果它确实有效,那么它可能是我们可能的解决方案之一。
- 即使我们有一个有效的表达式,我们也需要跟踪我们为获得这个表达式所做的删除操作的数量。这是由另一个名为rem_count的递归中传递的变量完成的。
- 一旦递归完成,我们将检查rem_count的当前值是否小于我们迄今为止为形成有效表达式所采取的最少步骤数,即全局最小值。如果不是这样的话,我们不会记录新的表达式,否则我们会记录它。
从实现的角度来看,我们可以做的一个小的优化就是在我们的算法中引入某种修剪。现在,我们只需到最后一步,即处理所有的括号,当我们处理完所有的括号后,我们检查我们的表达式是否可以被考虑。
我们必须等到最后才决定递归中形成的表达式是否是有效的表达式。有没有一种方法可以让我们从早期的一些递归路径中切断,因为它们不会导致一个解决方案?答案是肯定的!优化基于以下思想。
对于递归过程中遇到的左括号,如果我们决定考虑它,那么它可能会导致或可能不会导致无效的最终表达式。如果后面没有匹配的右括号,最终可能导致表达式无效。但是,我们不确定这是否会发生。
但是,对于右括号,如果我们决定将其作为最终表达式的一部分保留(请记住,对于每个括号,我们都有两个选项,要么保留它,要么删除它并进一步递归),并且到目前为止表达式中没有对应的左括号来匹配它,那么无论之后做什么,它都肯定会导致无效表达式。
( ( ) ) )
在这种情况下,第三个右括号将使表达式无效。不管之后会发生什么,这都会给我们一个无效的表达式,如果发生这种情况,我们不应该进一步递归,只需要修剪递归树。
这就是为什么,除了在我们当前正在处理的原始字符串/表达式中具有索引之外,并且到目前为止已经形成了表达式字符串之外,我们还跟踪左括号和右括号的数量。每当我们在表达式中保留左括号时,我们就增加它的计数器。对于右括号,我们检查right_count < left_count。如果是这种情况,那么我们只考虑右括号,并进一步递归。否则,我们不知道它会使表达式无效。这个简单的优化节省了很多运行时间。
现在,让我们看看这个算法的实现。
class Solution(object):
def __init__(self):
self.valid_expressions = None
self.min_removed = None
def reset(self):
self.valid_expressions = set()
self.min_removed = float("inf")
"""
string: The original string we are recursing on.
index: current index in the original string.
left: number of left parentheses till now.
right: number of right parentheses till now.
ans: the resulting expression in this particular recursion.
ignored: number of parentheses ignored in this particular recursion.
"""
def remaining(self, string, index, left_count, right_count, expr, rem_count):
# If we have reached the end of string.
if index == len(string):
# If the current expression is valid. The only scenario where it can be
# invalid here is if left > right. The other way around we handled early on in the recursion.
if left_count == right_count:
if rem_count <= self.min_removed:
# This is the resulting expression.
# Strings are immutable in Python so we move around a list in the recursion
# and eventually join to get the final string.
possible_ans = "".join(expr)
# If the current count of brackets removed < current minimum, ignore
# previous answers and update the current minimum count.
if rem_count < self.min_removed:
self.valid_expressions = set()
self.min_removed = rem_count
self.valid_expressions.add(possible_ans)
else:
current_char = string[index]
# If the current character is not a parenthesis, just recurse one step ahead.
if current_char != '(' and current_char != ')':
expr.append(current_char)
self.remaining(string, index + 1, left_count, right_count, expr, rem_count)
expr.pop()
else:
# Else, one recursion is with ignoring the current character.
# So, we increment the ignored counter and leave the left and right untouched.
self.remaining(string, index + 1, left_count, right_count, expr, rem_count + 1)
expr.append(current_char)
# If the current parenthesis is an opening bracket, we consider it
# and increment left and move forward
if string[index] == '(':
self.remaining(string, index + 1, left_count + 1, right_count, expr, rem_count)
elif right_count < left_count:
# If the current parenthesis is a closing bracket, we consider it only if we
# have more number of opening brackets and increment right and move forward.
self.remaining(string, index + 1, left_count, right_count + 1, expr, rem_count)
expr.pop()
def removeInvalidParentheses(self, s):
"""
:type s: str
:rtype: List[str]
"""
# Reset the class level variables that we use for every test case.
self.reset()
# Recursive call
self.remaining(s, 0, 0, 0, [], 0)
return list(self.valid_expressions)
复杂度分析
时间复杂度:O(2^N)。因为在最坏的情况下,表达式中只有左括号,对于每个括号,我们都有两个选项,即是删除还是考虑它。考虑到表达式有N括号,时间复杂性将为O(2^N)。
空间复杂度:O(N),因为我们使用的是递归解决方案,对于递归解决方案,在递归过程中,始终有堆栈空间用作内部函数状态保存到堆栈中。递归的最大深度决定了所使用的堆栈空间。因为我们一次处理一个字符,而递归的基本情况是当我们处理完表达式字符串的所有字符时,堆栈的大小将为O(n)。注意,我们不考虑存储有效表达式所需的空间。我们只计算中间过程的空间。
- 方法二:有限的回溯
虽然之前的解决方案在平台上得到了认可,但这是一个非常低效的解决方案,因为我们尝试从表达式中删除每个可能的括号,最后我们检查两件事:
表达式有效或无效
当前递归中删除的括号总数是否小于当前为止的全局最小值。
我们无法确定哪一个括号放错了位置,在问题陈述提出我们可以删除多个括号组合,最后得到一个有效的表达式。这意味着一个无效表达式可以有多个有效表达式,我们必须找到所有这些表达式。
所有这些有效表达式的一个共同点是,它们的长度都相同,即与原始表达式相比,所有这些表达式都将删除相同数量的字符。
如果我们能确定这个数呢?
如果除了确定要删除的字符数之外,我们还可以确定要从原始表达式中删除的左括号数和右括号数,以获得任何有效的表达式呢?
这将极大地减少计算量,从而导致运行时急剧下降。这样做的原因是,如果我们知道要从原始表达式中删除多少左括号和右括号以获得有效的表达式,那么我们将减少不需要的递归调用。
假设原始表达式是1000个字符,其中只有3个放错了位置(括号和2个放错了位置的)括号。在前面的解决方案中,我们最终将尝试删除左括号和右括号中的每一个,并尝试在末尾达到有效的表达式,而我们只应尝试删除3个(括号和2个)括号。
我们需要不多不少的获取有效表达式必须删除的(和)的确切数目。
让我们先看看如何找出给定表达式中左括号和右括号放错的数目,然后我们将稍微修改原始算法以合并这些计数。
- 我们从左边开始,一次处理一个括号的表达式。
- 假设我们遇到一个左括号,即(,它可能会导致或可能不会导致一个无效的表达式,因为表达式的其余部分的某个地方可能有一个匹配的右括号。这里,我们只需增加计数器来跟踪左括号的出现次数。left += 1
- 如果我们遇到一个右括号,这有两个含义:
- 要么是这个右括号没有匹配的左括号,在这种情况下,该表达式是无效的。当left == 0时,即没有不匹配的左括号可用时,就是这种情况。在这种情况下,我们增加另一个计数器叫right+=1来表示放错了位置的右括号。
- 或者,我们有一些未匹配的左括号来匹配这个右括号。当left > 0时就是这样。在这种情况下,我们只需减小我们使用的left计数器,即left -= 1。
- 继续处理字符串,直到处理完所有括号。
- 最后,左括号和右括号的值分别告诉我们不匹配(和)括号的数目。
现在我们有了这两个值,它们告诉我们为了使无效表达式有效而必须删除的左括号(和右括号)的总数,我们将修改上一个会话中讨论的原始算法,以避免不必要的递归。
算法:整个算法与以前完全相同。我们将纳入的变更如下:
- 递归的状态现在由五个不同的变量定义:
- index它表示我们必须在原始字符串中处理的当前字符。
- left_count它表示添加到我们正在构建的表达式中的左括号数。
- right_count它表示添加到我们正在构建的表达式中的右括号数。
- left_rem是要删除的左括号数。
- right_rem表示保留要删除的右括号数。总的来说,为了使最终表达式有效,left_rem == 0和right_rem == 0。
- 当我们决定不考虑括号时,即删除括号,不管是左括号还是右括号,我们也必须考虑它们相应的剩余计数。这意味着,如果left_rem > 0,我们只能放弃左括号;同样,对于右括号,我们将检查right_rem > 0。
- 检查括号没有变化。只有丢弃圆括号的条件才会改变。
- 表达式在基本情况下有效的条件现在将变为left_rem == 0 and right_rem == 0。注意,我们不必再检查left_count == right_count了,因为在有效表达式的情况下,在递归结束时,我们会删除所有放错位置或无效的括号。所以,只有当left_rem == 0 and right_rem == 0时,我们才需要检查。
这里最重要的是,我们已经完全摆脱了检查移除的括号数量是否小于当前的最小值。这样做的原因是我们总是在递归开始时删除相同数量的括号,这些括号是由left_rem + right_rem定义的。
现在让我们看看这个修改过的算法版本的实现。
class Solution:
def removeInvalidParentheses(self, s):
"""
:type s: str
:rtype: List[str]
"""
left = 0
right = 0
# First, we find out the number of misplaced left and right parentheses.
for char in s:
# Simply record the left one.
if char == '(':
left += 1
elif char == ')':
# If we don't have a matching left, then this is a misplaced right, record it.
right = right + 1 if left == 0 else right
# Decrement count of left parentheses because we have found a right
# which CAN be a matching one for a left.
left = left - 1 if left > 0 else left
result = {}
def recurse(s, index, left_count, right_count, left_rem, right_rem, expr):
# If we reached the end of the string, just check if the resulting expression is
# valid or not and also if we have removed the total number of left and right
# parentheses that we should have removed.
if index == len(s):
if left_rem == 0 and right_rem == 0:
ans = "".join(expr)
result[ans] = 1
else:
# The discard case. Note that here we have our pruning condition.
# We don't recurse if the remaining count for that parenthesis is == 0.
if (s[index] == '(' and left_rem > 0) or (s[index] == ')' and right_rem > 0):
recurse(s, index + 1,
left_count,
right_count,
left_rem - (s[index] == '('),
right_rem - (s[index] == ')'), expr)
expr.append(s[index])
# Simply recurse one step further if the current character is not a parenthesis.
if s[index] != '(' and s[index] != ')':
recurse(s, index + 1,
left_count,
right_count,
left_rem,
right_rem, expr)
elif s[index] == '(':
# Consider an opening bracket.
recurse(s, index + 1,
left_count + 1,
right_count,
left_rem,
right_rem, expr)
elif s[index] == ')' and left_count > right_count:
# Consider a closing bracket.
recurse(s, index + 1,
left_count,
right_count + 1,
left_rem,
right_rem, expr)
# Pop for backtracking.
expr.pop()
# Now, the left and right variables tell us the number of misplaced left and
# right parentheses and that greatly helps pruning the recursion.
recurse(s, 0, 0, 0, left, right, [])
return list(result.keys())
复杂度分析
时间复杂度:我们所执行的优化只是一种更好的修剪形式。在最坏的情况下,我们可以有(((((((((和left_rem = len(S)和在这种情况下我们可以丢弃所有字符,因为所有字符都放错了位置。在最坏的情况下,每个括号中仍然有两个选项,这给了我们O(2^n)的复杂性。
空间复杂度:空间复杂性与以前的解决方案保持相同,即O(N)。在到达基本情况之前,我们必须达到N的最大递归深度。注意,我们不考虑存储有效表达式所需的空间。我们只计算中间过程空间。