题目0076:最小覆盖子串

题目描述

给你一个字符串S、一个字符串T,请在字符串S里面找出:包含T所有字符的最小子串。

示例:

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"
说明:

如果S中不存这样的子串，则返回空字符串 ""。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

解题技巧

• 方法一:滑动窗口

本问题要求我们返回字符串s中包含字符串t的全部字符的最小窗口。我们称包含t的全部字母的窗口为可行窗口。

我们可以用滑动窗口的思想解决这个问题,在滑动窗口类型的问题中都会有两个指针。一个用于延伸现有窗口的r指针,和一个用于收缩窗口的l指针。在任意时刻,只有一个指针运动,而另一个保持静止。我们在s上滑动窗口,通过移动r指针不断扩张窗口。当窗口包含t全部所需的字符后,如果能收缩,我们就收缩窗口直到得到最小窗口。

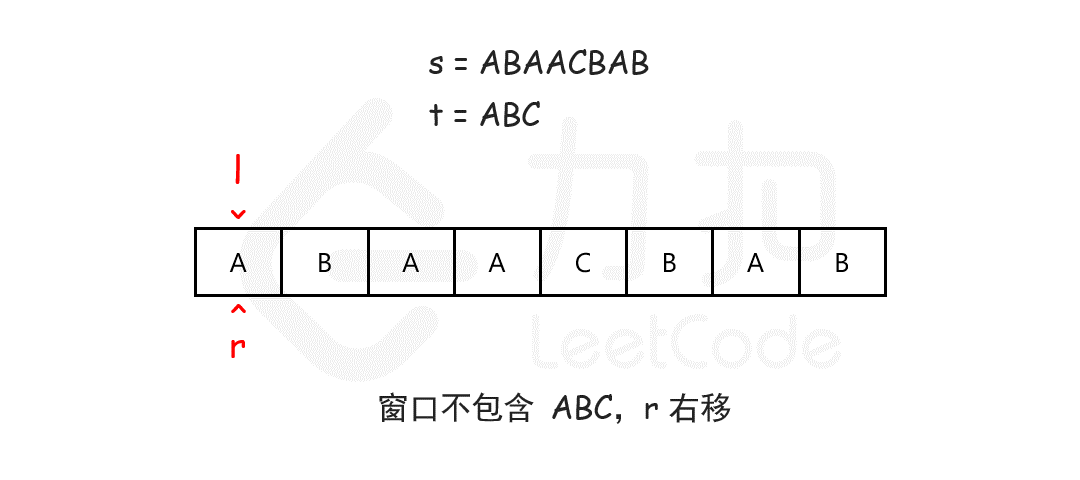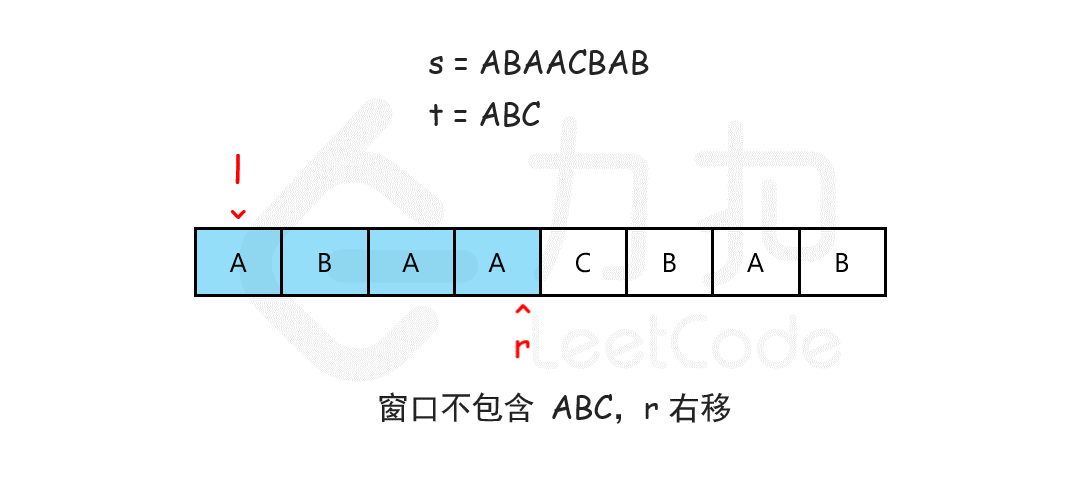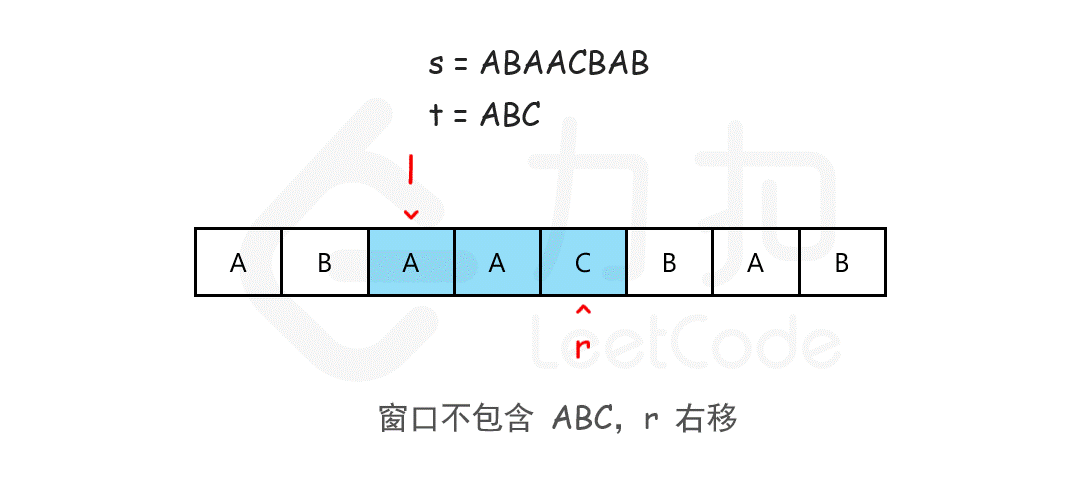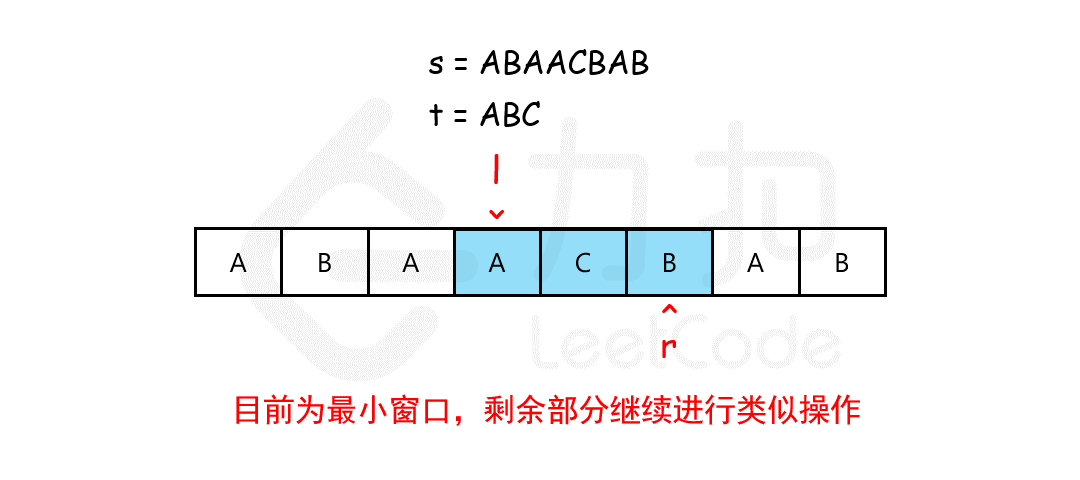
如何判断当前的窗口包含所有t所需的字符呢?我们可以用一个哈希表表示t中所有的字符以及它们的个数,用一个哈希表动态维护窗口中所有的字符以及它们的个数,如果这个动态表中包含t的哈希表中的所有字符，并且对应的个数都不小于t的哈希表中各个字符的个数,那么当前的窗口是可行的。

注意:这里t中可能出现重复的字符,所以我们要记录字符的个数。

考虑如何优化?如果$s = {\rm XX \cdots XABCXXXX}$,$t = {\rm ABC}$,那么显然${\rm [XX \cdots XABC]}$是第一个得到的可行区间,得到这个可行区间后,我们按照收缩窗口的原则更新左边界,得到最小区间。我们其实做了一些无用的操作,就是更新右边界的时候延伸进了很多无用的$\rm X$,更新左边界的时候收缩扔掉了这些无用的$\rm X$,做了这么多无用的操作,只是为了得到短短的$\rm ABC$。没错,其实在s中,有的字符我们是不关心的,我们只关心t中出现的字符,我们可不可以先预处理s,扔掉那些t中没有出现的字符,然后再做滑动窗口呢?也许你会说,这样可能出现$\rm XXABXXC$的情况,在统计长度的时候可以扔掉前两个$\rm X$,但是不扔掉中间的$\rm X$,怎样解决这个问题呢?优化后的时空复杂度又是多少?这里代码给出没有优化的版本,以上的三个问题留给读者思考,欢迎大家在评论区给出答案哟。

代码

class Solution {
public:
    unordered_map <char, int> ori, cnt;

    bool check() {
        for (const auto &p: ori) {
            if (cnt[p.first] < p.second) {
                return false;
            }
        }
        return true;
    }

    string minWindow(string s, string t) {
        for (const auto &c: t) {
            ++ori[c];
        }

        int l = 0, r = -1;
        int len = INT_MAX, ansL = -1, ansR = -1;

        while (r < int(s.size())) {
            if (ori.find(s[++r]) != ori.end()) {
                ++cnt[s[r]];
            }
            while (check() && l <= r) {
                if (r - l + 1 < len) {
                    len = r - l + 1;
                    ansL = l;
                }
                if (ori.find(s[l]) != ori.end()) {
                    --cnt[s[l]];
                }
                ++l;
            }
        }

        return ansL == -1 ? string() : s.substr(ansL, len);
    }
};

复杂度分析

时间复杂度:最坏情况下左右指针对s的每个元素各遍历一遍,哈希表中对s中的每个元素各插入、删除一次,对t中的元素各插入一次。每次检查是否可行会遍历整个t的哈希表,哈希表的大小与字符集的大小有关,设字符集大小为C,则渐进时间复杂度为$O(C\cdot |s| + |t|)$。

空间复杂度:这里用了两张哈希表作为辅助空间,每张哈希表最多不会存放超过字符集大小的键值对,我们设字符集大小为C，则渐进空间复杂度为O(C)。