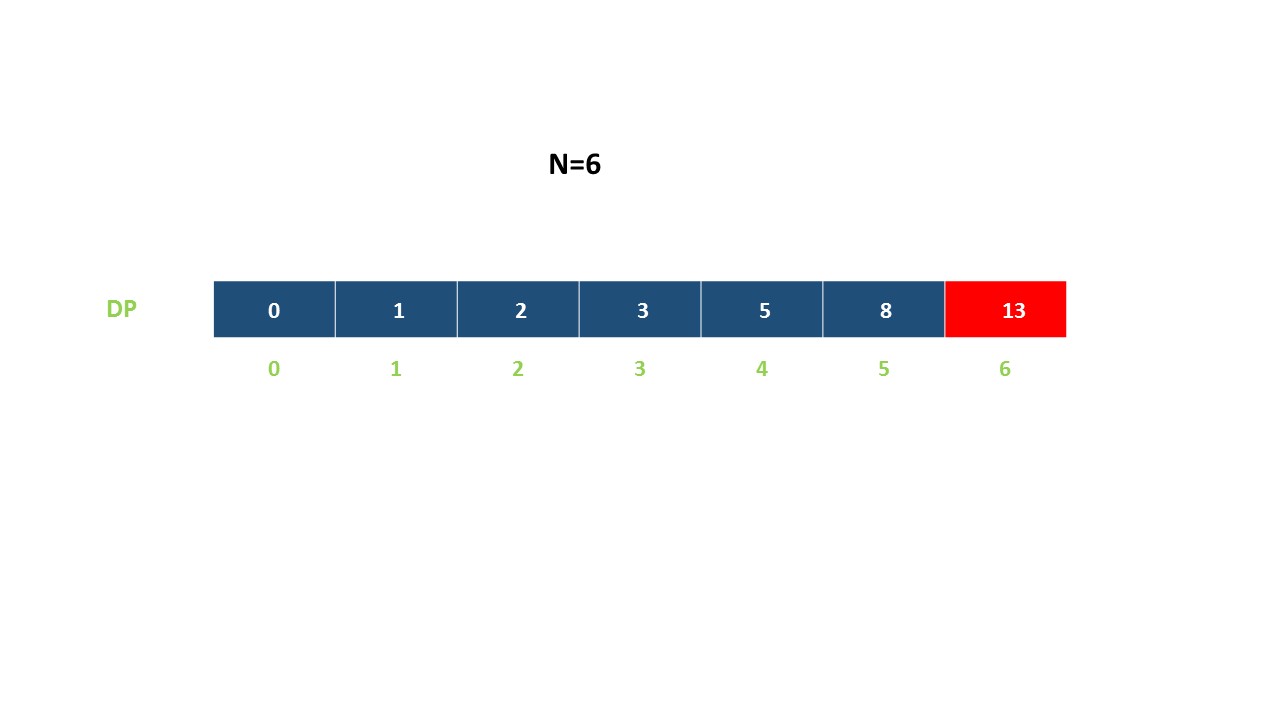
题目0070:爬楼梯

题目描述

假设你正在爬楼梯。需要n阶你才能到达楼顶。

每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?

注意:给定n是一个正整数。

示例1:

输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
    1. 1阶+1阶
    2. 2阶

示例 2:

输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
    1. 1阶+1阶+1阶
    2. 1阶+2阶
    3. 2阶+1阶

解题技巧

方法一:暴力法

在暴力法中,我们将会把所有可能爬的阶数进行组合,也就是1和2。而在每一步中我们都会继续调用climbStairsclimbStairs这个函数模拟爬1阶和2阶的情形,并返回两个函数的返回值之和。

$climbStairs(i,n)=climbStairs(i+1,n)+climbStairs(i+2,n)$

其中i定义了当前阶数,而n定义了目标阶数。

class Solution {
    public:
        int climbStairs(int n) {
            return climb_Stairs(0,n);
        }
        int climb_Stairs(int i,int n) {
            if(i>n) return 0;
            if(i==n) return 1;
            return climb_Stairs(i+1,n)+climb_Stairs(i+2,n);
        }
};

复杂度分析

时间复杂度: $O(2^n)$ ,树形递归的大小为 $2^n$ 。在n=5时的递归树将是这样的:

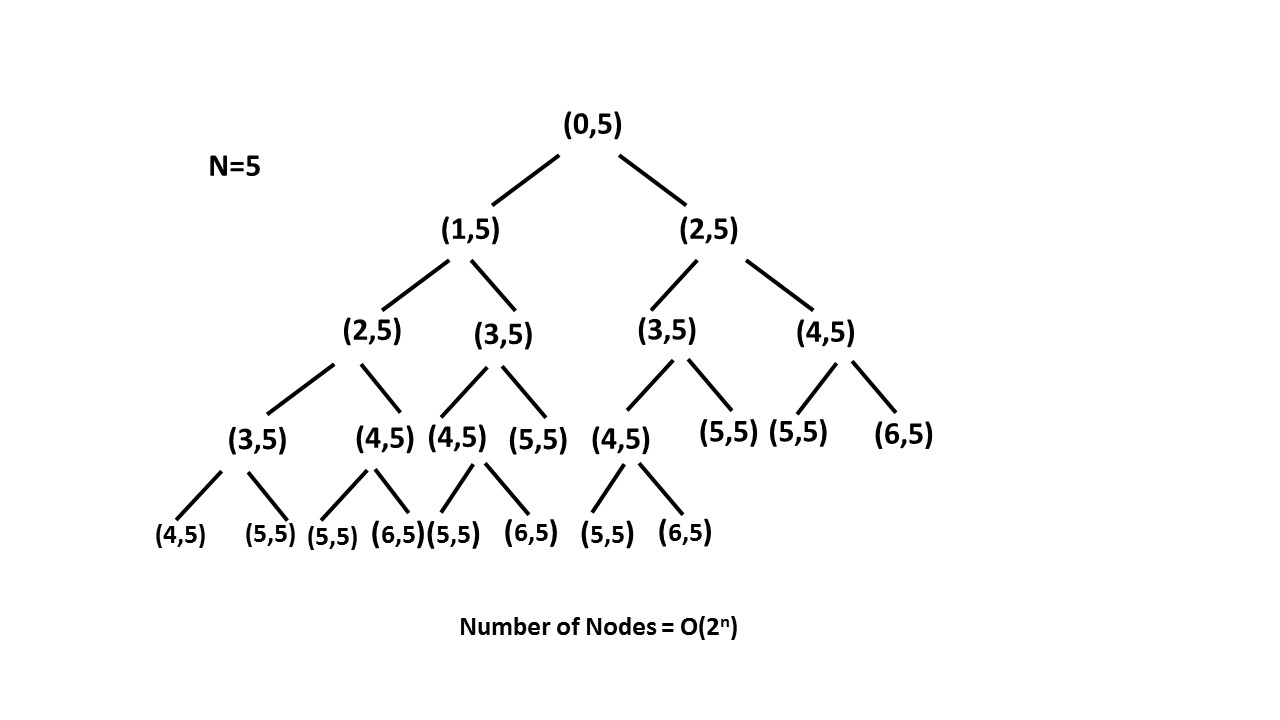
空间复杂度: $O(n)$ ,递归树的深度可以达到n。

方法二:记忆化递归

在上一种方法中,我们计算每一步的结果时出现了冗余。另一种思路是,我们可以把每一步的结果存储在memo数组之中,每当函数再次被调用,我们就直接从memo数组返回结果。

在memo数组的帮助下,我们得到了一个修复的递归树,其大小减少到n。

class Solution {
    public:
        int climbStairs(int n) {
            vector<int> memo;
            for(int i=0;i<n;i++) memo.push_back(0);
            return climb_Stairs(0,n,memo);

        }
        int climb_Stairs(int i,int n, vector<int>& memo) {
            if(i>n) return 0;
            if(i==n) return 1;
            if(memo[i]>0) return memo[i];
            memo[i] = climb_Stairs(i+1,n,memo)+climb_Stairs(i+2,n,memo);
            return memo[i];
        }
};

复杂度分析

时间复杂度: $O(n)$ ,树形递归的大小可以达到n。

空间复杂度: $O(n)$ ,递归树的深度可以达到n。

方法三:动态规划

不难发现,这个问题可以被分解为一些包含最优子结构的子问题,即它的最优解可以从其子问题的最优解来有效地构建,我们可以使用动态规划来解决这一问题。

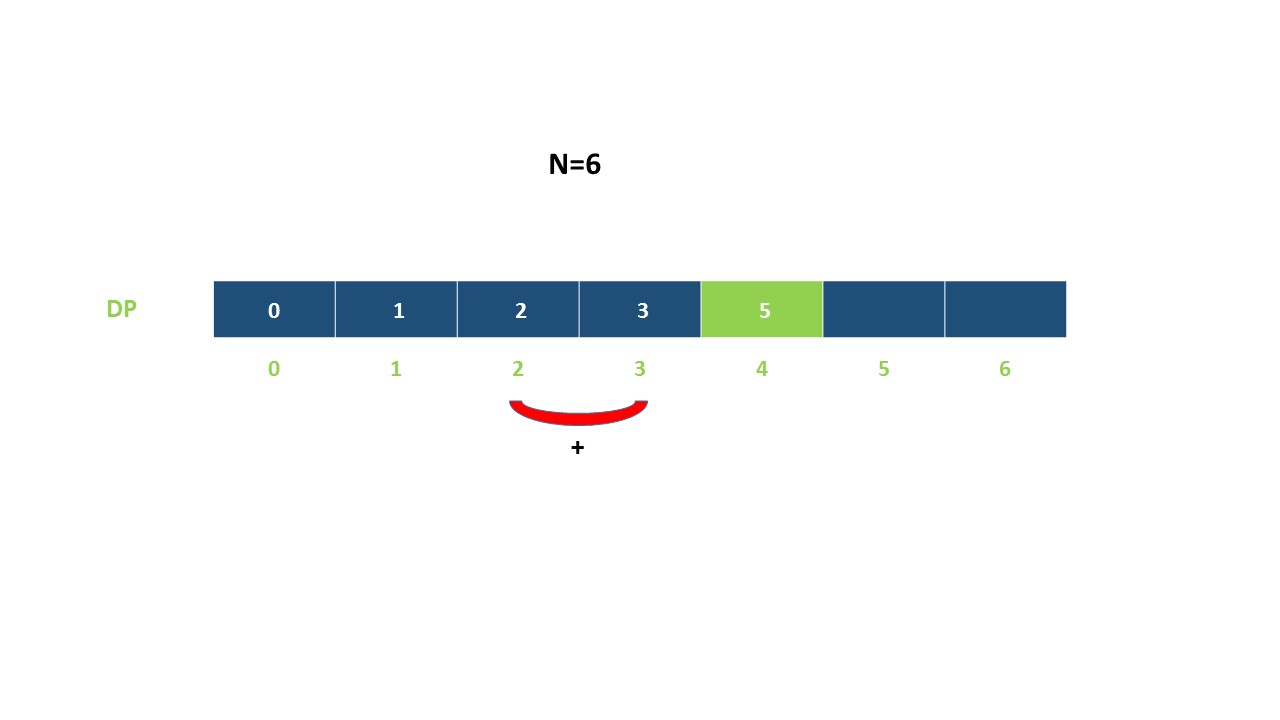
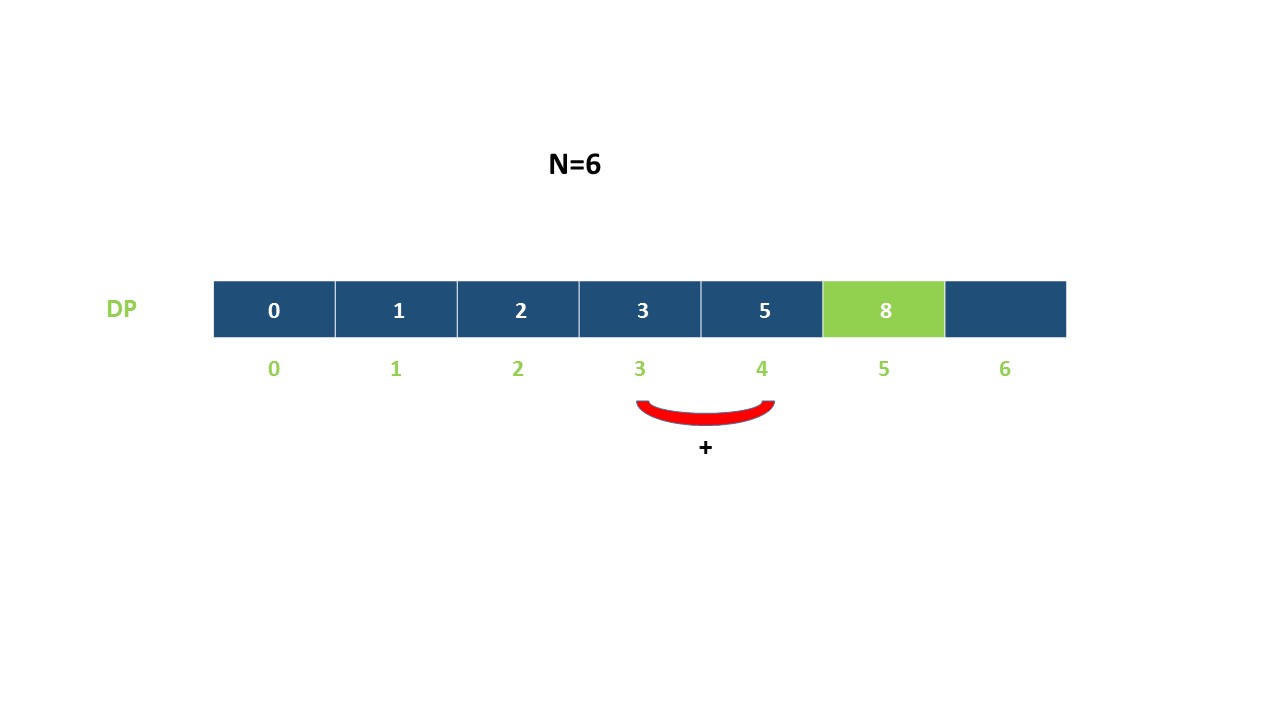
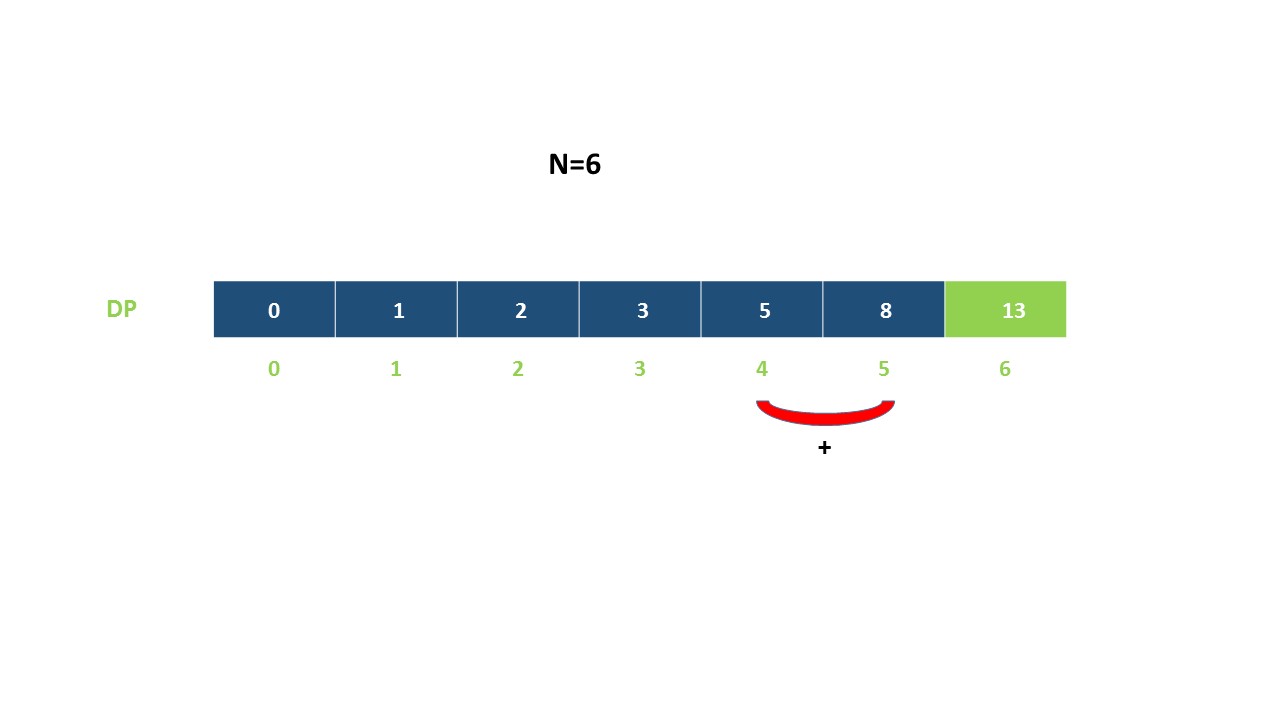
第i阶可以由以下两种方法得到:

在第(i-1)阶后向上爬一阶。

在第(i-2)阶后向上爬2阶。

所以到达第i阶的方法总数就是到第(i-1)阶和第(i-2)阶的方法数之和。

令dp[i]表示能到达第i阶的方法总数:

$dp[i]=dp[i-1]+dp[i-2]$

示例:

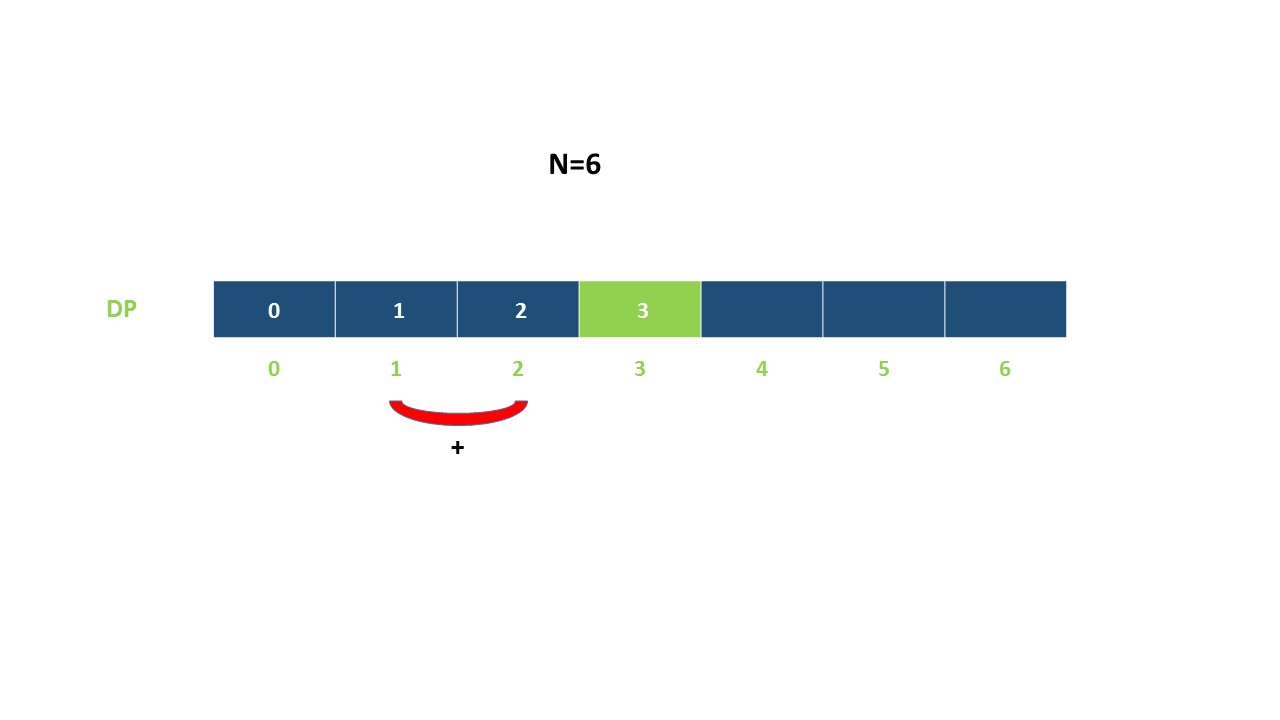
class Solution {
    public:
        int climbStairs(int n) {
            vector<int> memo;
            memo.push_back(1);
            memo.push_back(1);
            for(int i=2;i<=n;i++) memo.push_back(memo[i-1]+memo[i-2]);
            return memo[n];        
        }  
};

复杂度分析

时间复杂度: $O(n)$ ,单循环到n。

空间复杂度: $O(n)$ ,dp数组用了n的空间。

方法四:斐波那契数

在上述方法中,我们使用dp数组,其中 $dp[i]=dp[i-1]+dp[i-2]$ 。可以很容易通过分析得出dp[i]其实就是第i个斐波那契数。

$Fib(n)=Fib(n-1)+Fib(n-2)$

现在我们必须找出以1和2作为第一项和第二项的斐波那契数列中的第n个数,也就是说 $Fib(1)=1$ 且 $Fib(2)=2$ 。

class Solution {
    public:
        int climbStairs(int n) {
            if(n==1 or n==2) return n;
            int first=1,second=2;
            for(int i=3;i<=n;i++){
                int third = first+second;
                first = second;
                second=third;
            }
            return second;        
        }
};

复杂度分析

时间复杂度: $O(n)$ ,单循环到n,需要计算第n个斐波那契数。

空间复杂度: $O(1)$ ,使用常量级空间。

方法五:Binets方法

这里有一种有趣的解法,它使用矩阵乘法来得到第n个斐波那契数。矩阵形式如下:

$\left[ {\begin{array}{cc} F_{n+1} & F_n \\ F_n & F_{n-1} \end{array} } \right] = \left[ {\begin{array}{cc} 1 & 1 \\ 1 & 0 \end{array} } \right]$

令 $Q=\left[ {\begin{array}{cc} F_{n+1} & F_n \\ F_n & F_{n-1} \end{array} } \right]$ 。按照此方法,第n个斐波那契数可以由 $Q^{n-1}[1,1]$ 给出。

让我们试着证明一下。

我们可以使用数学归纳法来证明这一方法。易知,该矩阵给出了第3项(基本情况)的正确结果。由于 $Q^2 = \left[ {\begin{array}{cc} 2 & 1 \\ 1 & 1 \end{array} } \right]$ 。这证明基本情况是成立的。

假设此方法适用于查找第n个斐波那契数,即 $F_n=Q^{n-1}[1,1]$ ,那么:

$Q^{n-1}=\left[ {\begin{array}{cc} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \end{array} } \right]$

现在,我们需要证明在上述两个条件为真的情况下,该方法可以有效找出第(n+1)个斐波那契数,即 $F_{n+1}=Q^{n}[1,1]$ 。

证明:

$<span><span class="MathJax_Preview">Q^{n} = \left[ {\begin{array}{cc} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \end{array} } \right]\left[ {\begin{array}{cc} 1 & 1 \\ 1 & 0 \end{array} } \right]</span><script type="math/tex">Q^{n} = \left[ {\begin{array}{cc} F_{n} & F_{n-1} \\ F_{n-1} & F_{n-2} \end{array} } \right]\left[ {\begin{array}{cc} 1 & 1 \\ 1 & 0 \end{array} } \right]$ .

$Q^{n} = \left[ {\begin{array}{cc} F_{n}+F_{n-1} & F_n \\ F_{n-1}+F_{n-2} & F_{n-1} \end{array} } \right]$

$Q^{n} = \left[ {\begin{array}{cc} F_{n+1} & F_n \\ F_n & F_{n-1} \end{array} } \right]$

从而, $F_{n+1}=Q^{n}[1,1]$ ,得证。

我们需要为我们的问题做的唯一改动就是将斐波那契数列的初始项修改为2和1来代替原来的1和0 。或者,另一种方法是使用相同的初始矩阵Q并使用 $result = Q^{n}[1,1]$ r得出最后结果。发生这种情况的原因是我们必须使用原斐波那契数列的第2项和第3项作为初始项。

import numpy as np
class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        multi = np.array([[1,1],[1,0]])
        temp_ = multi
        for i in range(n-1):
            temp_ = temp_.dot(multi)
        return temp_[0][0]

复杂度分析:

时间复杂度: $O(log(n))$ ,遍历 $log(n)$ 位。

空间复杂度: $O(1)$ ,使用常量级空间。

对时间复杂度的证明:

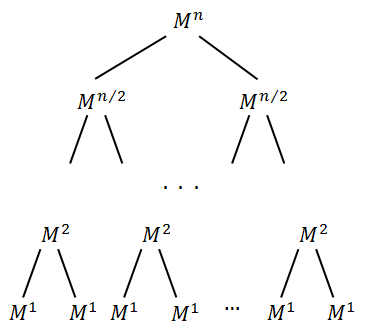
假设我们需要计算矩阵M的n次幂。假设,n是2的幂。因此, $n = 2^i,i\in\mathbb{N}$ ,其中 $\mathbb{N}$ 表示自然数的集合(包括0)。我们可以用树形结构进行表示:

这意味着: $M^n = M^{n/2}.M^{n/2} = .... = \prod_{1}^{n} M^{1}$

所以,要计算 $M^{n}$ ,我们先要计算 $M^{n/2}$ 并将其与自身相乘。而为了计算 $M^{n/2}$ ,我们需要对 $M^{n/4}$ 进行类似的操作,并依此类推。

显然,树的高度为 $log_{2}$ 。

让我们来估计一下 $M^{n}$ 计算所需要的时间。矩阵M在幂运算过程中大小保持不变。因此,进行两矩阵幂乘的空间复杂度是 $O(1)$ 。我们需要执行 $log_2{n}$ 次这样的乘法。所以,计算 $M^{n}$ 的时间复杂度为 $O(log_{2}n)$ 。

如果数字 n不是2的幂,我们可以使用其二进制表示将其转化为 2 的幂次项之和:

$n= \sum_{p\in P} 2^{p}, \text{where }P\subset\mathbb{N}$

因此,我们可以使用以下方法获得最终结果:

$M^{n} = \prod_{p\in P} M^{2^{p}}$

这是我们在实现中使用的方法。同样,时间复杂度仍为 $O(log_{2}n)$ ,因为乘法次数的限制为 $O(log_{2}n)$ 。

方法六:斐波那契公式

我们可以使用这一公式来找出第n个斐波那契数:

$F_n = 1/\sqrt{5}\left[ \left(\frac{1+\sqrt{5}}{2}\right)^{n} - \left(\frac{1-\sqrt{5}}{2}\right)^{n} \right]$

对于给定的问题,斐波那契序列将会被定义为 $F_0 = 1,F_1= 1,F_2= 2,F_{n+2}= F_{n+1} + F_n$ 。尝试解决这一递归公式的标准方法是设出 $F_n$ ,其形式为 $F_n= a^n$ 。然后,自然有 $F_{n+1} = a^{n+1}$ 和 $F_{n+2}= a^{n+2}$ ,所以方程可以写作 $a^{n+2}= a^{n+1}+ a^n$ 。如果我们对整个方程进行约分,可以得到 $a^2= a + 1$ 或者写成二次方程形式 $a^2 - a- 1= 0$ 。

对二次公式求解,我们得到:

$a=1/\sqrt{5}\left(\left(\frac{1\pm \sqrt{5}}{2}\right)\right)$

一般解采用以下形式:

$F_n = A\left(\frac{1+\sqrt{5}}{2}\right)^{n} + B\left(\frac{1-\sqrt{5}}{2}\right)^{n}$

n=0时,有A + B = 1
n=1 时,有¥A\left(\frac{1+\sqrt{5}}{2}\right) + B\left(\frac{1-\sqrt{5}}{2}\right) = 1$

解上述等式,我们得到:

$A = \left(\frac{1+\sqrt{5}}{2\sqrt{5}}\right), B = \left(\frac{1-\sqrt{5}}{2\sqrt{5}}\right)$

将 $A$ 和 $B$ 的这些值带入上述的一般解方程中,可以得到:

$F_n = 1/\sqrt{5}\left( \left(\frac{1+\sqrt{5}}{2}\right)^{n+1} - \left(\frac{1-\sqrt{5}}{2}\right)^{n+1} \right)$

class Solution {
    public:
        int climbStairs(int n) {
            double sqrt5 = sqrt(5);
            double fibn=pow((1+sqrt5)/2,n+1)-pow((1-sqrt5)/2,n+1);
            return (int)(fibn/sqrt5);
        }
};

复杂度分析:

时间复杂度: $O(log(n))$ ,pow方法将会用去 $log(n)$ 的时间。

空间复杂度: $O(1)$ ,使用常量级空间。