题目0064:最小路径和

题目描述

给定一个包含非负整数的mxn网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。

说明:每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

解题技巧

• 方法1:暴力

暴力就是利用递归,对于每个元素我们考虑两条路径,向右走和向下走,在这两条路径中挑选路径权值和较小的一个。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        return calculate(grid, 0, 0);
    }
    int calculate(vector<vector<int>>& grid, int i, int j) {
        if (i == grid.size() || j == grid[0].size()) return 0x3f3f3f3f;
        if (i == grid.size() - 1 && j == grid[0].size() - 1) return grid[i][j];
        return grid[i][j] + min(calculate(grid, i + 1, j), calculate(grid, i, j + 1));
    }
};

复杂度分析

时间复杂度:$O\big(2^{m+n}\big)$。每次移动最多可以有两种选择。

空间复杂度:O(m+n)。递归的深度是m+n。

• 方法2:二维动态规划

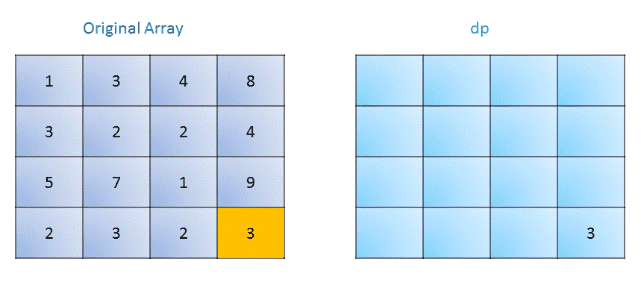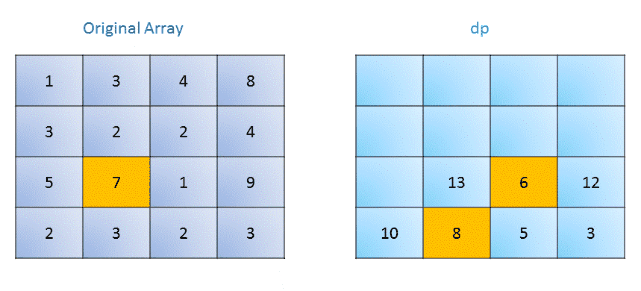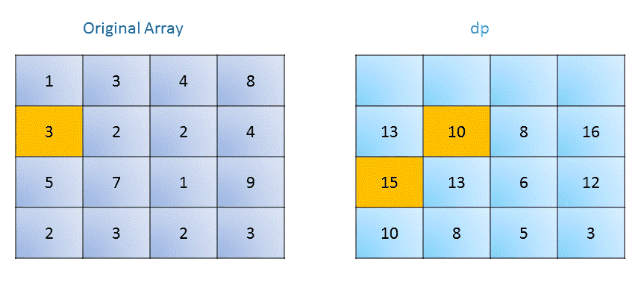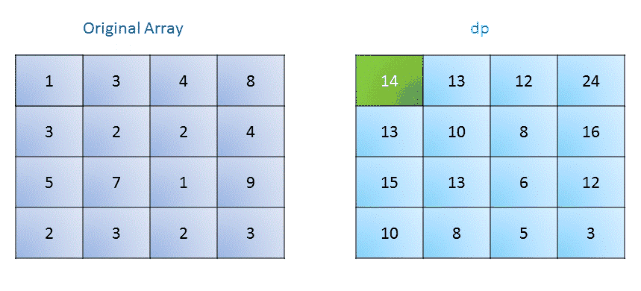
算法:我们新建一个额外的dp数组,与原矩阵大小相同。在这个矩阵中,dp(i,j)表示从坐标(i,j)到右下角的最小路径权值。我们初始化右下角的dp值为对应的原矩阵值,然后去填整个矩阵,对于每个元素考虑移动到右边或者下面,因此获得最小路径和我们有如下递推公式:

注意边界情况。下图描述了这个过程:

public class Solution {
    public int minPathSum(int[][] grid) {
        int[][] dp = new int[grid.length][grid[0].length];
        for (int i = grid.length - 1; i >= 0; i--) {
            for (int j = grid[0].length - 1; j >= 0; j--) {
                if(i == grid.length - 1 && j != grid[0].length - 1)
                    dp[i][j] = grid[i][j] +  dp[i][j + 1];
                else if(j == grid[0].length - 1 && i != grid.length - 1)
                    dp[i][j] = grid[i][j] + dp[i + 1][j];
                else if(j != grid[0].length - 1 && i != grid.length - 1)
                    dp[i][j] = grid[i][j] + Math.min(dp[i + 1][j], dp[i][j + 1]);
                else
                    dp[i][j] = grid[i][j];
            }
        }
        return dp[0][0];
    }
}

复杂度分析

时间复杂度:O(mn)。遍历整个矩阵恰好一次。

空间复杂度:O(mn)。额外的一个同大小矩阵。

• 方法3:一维动态规划

算法:在上个解法中,我们可以用一个一维数组来代替二维数组,dp数组的大小和行大小相同。这是因为对于某个固定状态,只需要考虑下方和右侧的节点。首先初始化dp数组最后一个元素是右下角的元素值,然后我们向左移更新每个dp(j)为:

我们对于每一行都重复这个过程,然后向上一行移动,计算完成后dp(0)就是最后的结果。

public class Solution {
   public int minPathSum(int[][] grid) {
       int[] dp = new int[grid[0].length];
       for (int i = grid.length - 1; i >= 0; i--) {
           for (int j = grid[0].length - 1; j >= 0; j--) {
               if(i == grid.length - 1 && j != grid[0].length - 1)
                   dp[j] = grid[i][j] +  dp[j + 1];
               else if(j == grid[0].length - 1 && i != grid.length - 1)
                   dp[j] = grid[i][j] + dp[j];
               else if(j != grid[0].length - 1 && i != grid.length - 1)
                   dp[j] = grid[i][j] + Math.min(dp[j], dp[j + 1]);
               else
                   dp[j] = grid[i][j];
           }
       }
       return dp[0];
   }
}

复杂度分析

时间复杂度:O(mn)。遍历整个矩阵恰好一次。

空间复杂度:O(n)。额外的一维数组,和一行大小相同。

• 方法4:动态规划(不需要额外存储空间)

算法:和方法2相同,惟一的区别是,不需要用额外的dp数组,而是在原数组上存储,这样就不需要额外的存储空间。递推公式如下:

public class Solution {
    public int minPathSum(int[][] grid) {
        for (int i = grid.length - 1; i >= 0; i--) {
            for (int j = grid[0].length - 1; j >= 0; j--) {
                if(i == grid.length - 1 && j != grid[0].length - 1)
                    grid[i][j] = grid[i][j] +  grid[i][j + 1];
                else if(j == grid[0].length - 1 && i != grid.length - 1)
                    grid[i][j] = grid[i][j] + grid[i + 1][j];
                else if(j != grid[0].length - 1 && i != grid.length - 1)
                    grid[i][j] = grid[i][j] + Math.min(grid[i + 1][j],grid[i][j + 1]);
            }
        }
        return grid[0][0];
    }
}

复杂度分析

时间复杂度:O(mn)。遍历整个矩阵恰好一次。

空间复杂度:O(1)。不需要额外空间。