题目0056:合并区间

题目描述

给出一个区间的集合,请合并所有重叠的区间。

示例1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

解题技巧

• 方法一:排序

如果我们按照区间的左端点排序,那么在排完序的列表中,可以合并的区间一定是连续的。如下图所示,标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间,它们在排完序的列表中是连续的:

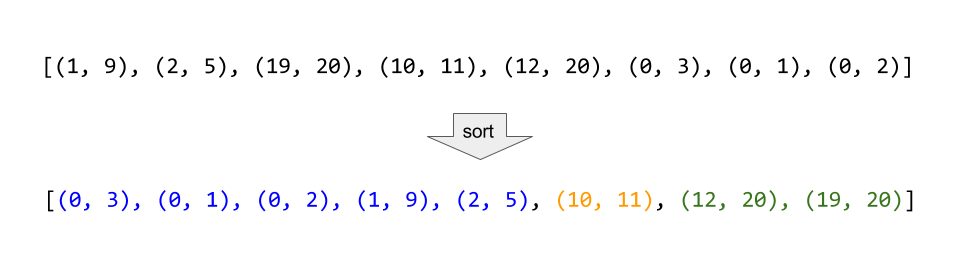
算法:我们用数组 merged 存储最终的答案。

首先,我们将列表中的区间按照左端点升序排序。然后我们将第一个区间加入merged数组中,并按顺序依次考虑之后的每个区间:

如果当前区间的左端点在数组merged中最后一个区间的右端点之后,那么它们不会重合,我们可以直接将这个区间加入数组merged的末尾;

否则,它们重合,我们需要用当前区间的右端点更新数组merged中最后一个区间的右端点,将其置为二者的较大值。

正确性证明

上述算法的正确性可以用反证法来证明:在排完序后的数组中,两个本应合并的区间没能被合并,那么说明存在这样的三元组(i, j, k)以及数组中的三个区间a[i], a[j], a[k]满足i< j < k并且(a[i], a[k])可以合并,但(a[i], a[j])和(a[j], a[k])不能合并。这说明它们满足下面的不等式:

a[i].end<a[j].start(a[i]和 a[j] 不能合并)
a[j].end<a[k].start(a[j]和 a[k] 不能合并)
a[i].end≥a[k].start(a[i]和 a[k] 可以合并)

我们联立这些不等式(注意还有一个显然的不等式$a[j].start \leq a[j].end$,可以得到:

产生了矛盾!这说明假设是不成立的。因此,所有能够合并的区间都必然是连续的。

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x: x[0])

        merged = []
        for interval in intervals:
            # 如果列表为空，或者当前区间与上一区间不重合，直接添加
            if not merged or merged[-1][1] < interval[0]:
                merged.append(interval)
            else:
                # 否则的话，我们就可以与上一区间进行合并
                merged[-1][1] = max(merged[-1][1], interval[1])
        return merged

复杂度分析

时间复杂度:$O(n\log n)$,其中n为区间的数量。除去排序的开销,我们只需要一次线性扫描,所以主要的时间开销是排序的$O(n\log n)$。

空间复杂度:$O(\log n)$,其中n为区间的数量。这里计算的是存储答案之外,使用的额外空间。$O(\log n)$即为排序所需要的空间复杂度。