题目0053:最大子序和

题目描述

给定一个整数数组nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组[4,-1,2,1]的和最大,为6。

进阶:如果你已经实现复杂度为O(n)的解法,尝试使用更为精妙的分治法求解。

解题技巧

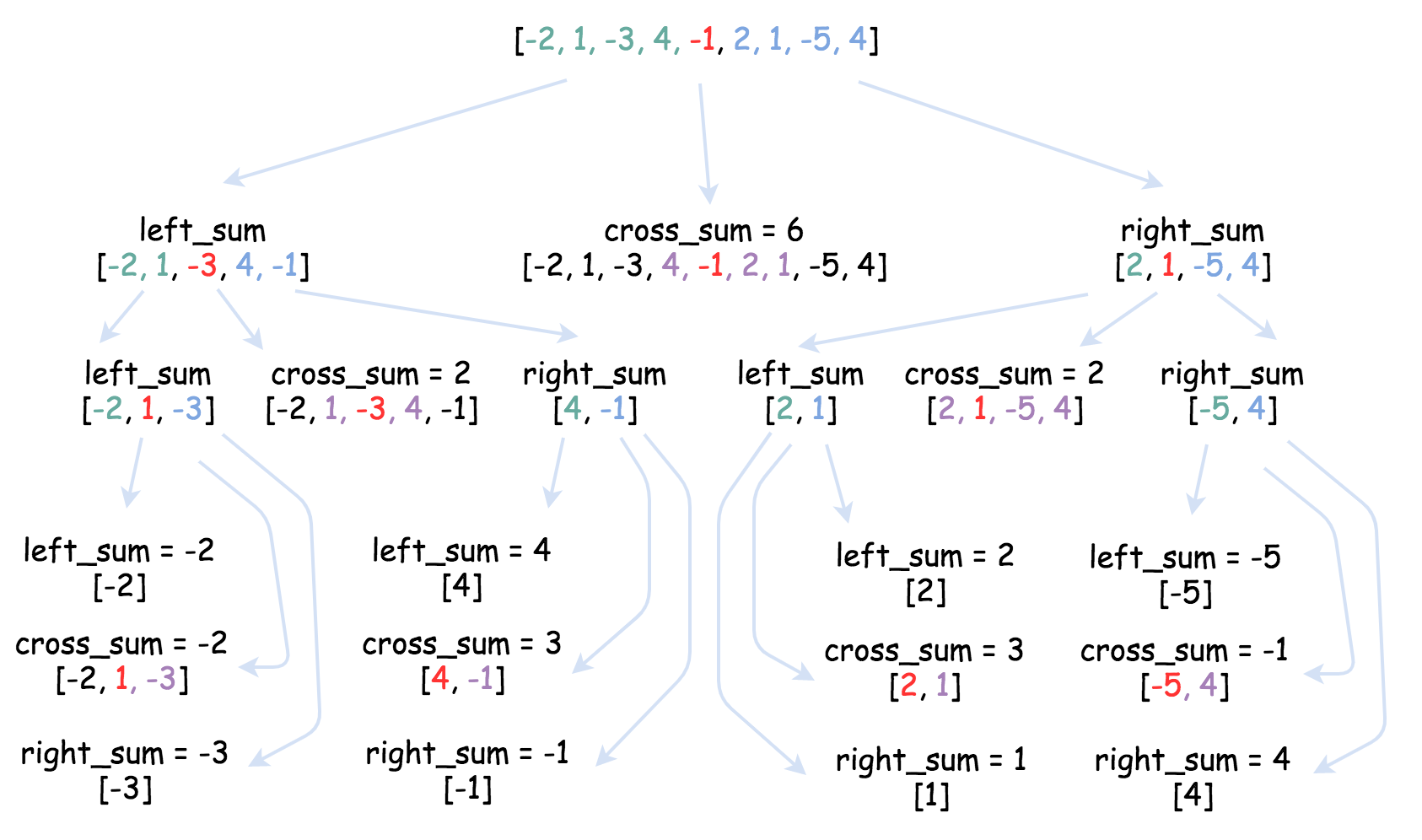
• 方法一:分治法

这个是使用分治法解决问题的典型的例子,并且可以用与合并排序相似的算法求解。下面是用分治法解决问题的模板：

定义基本情况。

将问题分解为子问题并递归地解决它们。

合并子问题的解以获得原始问题的解。

算法:当最大子数组有n个数字时:

若n==1,返回此元素。

left_sum为最大子数组前n/2个元素,在索引为(left + right)/2的元素属于左子数组。

right_sum为最大子数组的右子数组,为最后n/2的元素。

cross_sum是包含左右子数组且含索引(left + right)/2的最大值。

class Solution:
    def cross_sum(self, nums, left, right, p): 
        if left == right:
            return nums[left]

        left_subsum = float('-inf')
        curr_sum = 0
        for i in range(p, left - 1, -1):
            curr_sum += nums[i]
            left_subsum = max(left_subsum, curr_sum)

        right_subsum = float('-inf')
        curr_sum = 0
        for i in range(p + 1, right + 1):
            curr_sum += nums[i]
            right_subsum = max(right_subsum, curr_sum)

        return left_subsum + right_subsum   

    def helper(self, nums, left, right): 
        if left == right:
            return nums[left]

        p = (left + right) // 2

        left_sum = self.helper(nums, left, p)
        right_sum = self.helper(nums, p + 1, right)
        cross_sum = self.cross_sum(nums, left, right, p)

        return max(left_sum, right_sum, cross_sum)

    def maxSubArray(self, nums: 'List[int]') -> 'int':
        return self.helper(nums, 0, len(nums) - 1)

复杂度分析:

时间复杂度:$\mathcal{O}(N \log N)$。

空间复杂度:$\mathcal{O}(\log N)$,递归时栈使用的空间。

• 方法二:贪心

使用单个数组作为输入来查找最大(或最小)元素(或总和)的问题,贪心算法是可以在线性时间解决的方法之一。每一步都选择最佳方案,到最后就是全局最优的方案。

算法:该算法通用且简单：遍历数组并在每个步骤中更新:

当前元素

当前元素位置的最大和

迄今为止的最大和

class Solution:
    def maxSubArray(self, nums: 'List[int]') -> 'int':
        n = len(nums)
        curr_sum = max_sum = nums[0]

        for i in range(1, n):
            curr_sum = max(nums[i], curr_sum + nums[i])
            max_sum = max(max_sum, curr_sum)

        return max_sum

复杂度分析

时间复杂度:$\mathcal{O}(N)$。只遍历一次数组。

空间复杂度:$\mathcal{O}(1)$,只使用了常数空间。

• 方法三:动态规划(Kadane算法）

算法:在整个数组或在固定大小的滑动窗口中找到总和或最大值或最小值的问题可以通过动态规划(DP)在线性时间内解决。

有两种标准DP方法适用于数组:

常数空间,沿数组移动并在原数组修改。

线性空间,首先沿left->right方向移动,然后再沿right->left方向移动。 合并结果。

我们在这里使用第一种方法,因为可以修改数组跟踪当前位置的最大和。下一步是在知道当前位置的最大和后更新全局最大和。

class Solution:
    def maxSubArray(self, nums: 'List[int]') -> 'int':
        n = len(nums)
        max_sum = nums[0]
        for i in range(1, n):
            if nums[i - 1] > 0:
                nums[i] += nums[i - 1] 
            max_sum = max(nums[i], max_sum)

        return max_sum

复杂度分析

时间复杂度:$\mathcal{O}(N)$。只遍历了一次数组。

空间复杂度:$\mathcal{O}(1)$,使用了常数的空间。