题目0019:删除链表的倒数第N个节点
题目描述
给定一个链表,删除链表的倒数第n个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5,和n=2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:给定的n保证是有效的。
进阶:你能尝试使用一趟扫描实现吗?
解答技巧
- 方法一:两次遍历算法
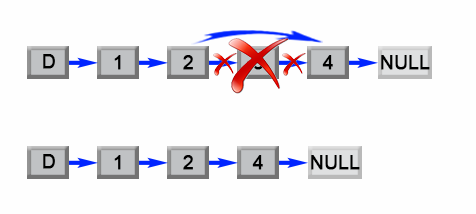
我们注意到这个问题可以容易地简化成另一个问题:删除从列表开头数起的第(L-n+1)个结点,其中L是列表的长度。只要我们找到列表的长度L,这个问题就很容易解决。
首先我们将添加一个哑结点作为辅助,该结点位于列表头部。哑结点用来简化某些极端情况,例如列表中只含有一个结点,或需要删除列表的头部。在第一次遍历中,我们找出列表的长度L。然后设置一个指向哑结点的指针,并移动它遍历列表,直至它到达第(L-n)个结点那里。我们把第(L-n)个结点的next指针重新链接至第(L-n+2)个结点,完成这个算法。
图1. 删除列表中的第L-n+1个元素
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
dummy = ListNode(0)
dummy.next=head
length = 0;
first = head;
while first is not None:
length = length +1
first = first.next
length = length-n;
first = dummy;
while length>0:
length = length-1
first = first.next
first.next = first.next.next;
return dummy.next;
复杂度分析:
时间复杂度:O(L),该算法对列表进行了两次遍历,首先计算了列表的长度L其次找到第(L-n)个结点。操作执行了2L-n步,时间复杂度为O(L)。
空间复杂度:O(1),我们只用了常量级的额外空间。
- 方法二:一次遍历算法
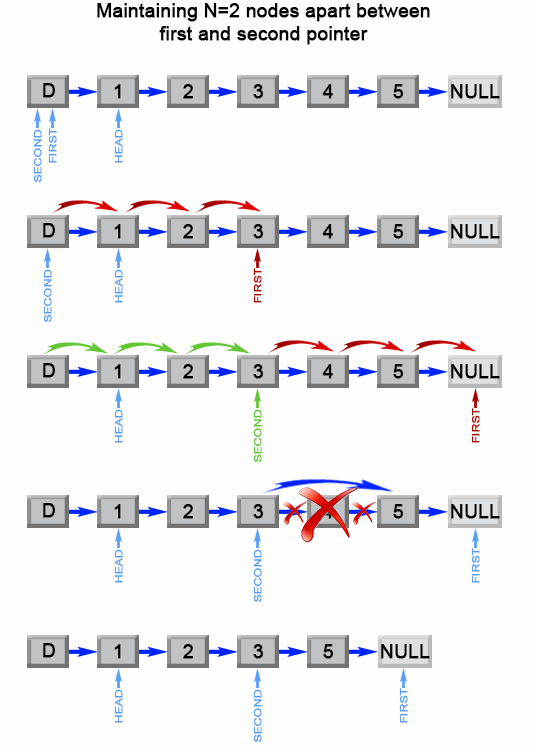
上述算法可以优化为只使用一次遍历。我们可以使用两个指针而不是一个指针,第一个指针从列表的开头向前移动n+1步,而第二个指针将从列表的开头出发。现在,这两个指针被n个结点分开。我们通过同时移动两个指针向前来保持这个恒定的间隔,直到第一个指针到达最后一个结点。此时第二个指针将指向从最后一个结点数起的第n个结点。我们重新链接第二个指针所引用的结点的next指针指向该结点的下下个结点。
图2. 删除链表的倒数第 N 个元素
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
// Advances first pointer so that the gap between first and second is n nodes apart
for (int i = 1; i <= n + 1; i++) {
first = first.next;
}
// Move first to the end, maintaining the gap
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
复杂度分析:
时间复杂度:O(L),该算法对含有L个结点的列表进行了一次遍历。因此时间复杂度为O(L)。
空间复杂度:O(1),我们只用了常量级的额外空间。