题目0005:最长回文子串

题目描述

给定一个字符串s,找到s中最长的回文子串。你可以假设s的最大长度为1000。

示例1:

输入: "babad"

输出: "bab"

注意: "aba" 也是一个有效答案。

示例2:

输入: "cbbd"

输出: "bb"

解答技巧

方法一:最长公共子串

有些人会忍不住提出一个快速的解决方案,不幸的是,这个解决方案有缺陷(但是可以很容易地纠正):

反转S,使之变成S'。找到S和S'之间最长的公共子串,这也必然是最长的回文子串。这似乎是可行的,让我们看看下面的一些例子。

例如,S="caba",S'="abac":S以及S'之间的最长公共子串为"aba",恰恰是答案。让我们尝试一下这个例子:S=“abacdfgdcaba”,S'="abacdgfdcaba":S以及S'之间的最长公共子串为"abacd"。显然,这不是回文。

我们可以看到,当S的其他部分中存在非回文子串的反向副本时,最长公共子串法就会失败。为了纠正这一点,每当我们找到最长的公共子串的候选项时,都需要检查子串的索引是否与反向子串的原始索引相同。如果相同,那么我们尝试更新目前为止找到的最长回文子串;如果不是,我们就跳过这个候选项并继续寻找下一个候选。

class Solution {
    public:
        string longestPalindrome(string s) {
            if(s=="") return "";
            string reverse;
            reverse.assign(s.rbegin(), s.rend());

            int length=s.length();
            int maxLen=0,maxEnd=0;
            vector<int> arr;
            for(int i=0;i<length;++i) arr.push_back(0);

            for(int i=0;i<length;i++){
                for(int j=length-1;j>=0;j--){
                    if(s[i]==reverse[j]) {
                    if(i==0 || j==0)
                        arr[j]=1;
                    else
                        arr[j] = arr[j - 1] + 1;
                }
                else arr[j]=0;
                if (arr[j] > maxLen) {
                    int beforeRev = length - 1 - j;
                    if (beforeRev + arr[j] - 1 == i) {
                        maxLen = arr[j];
                        maxEnd = i;
                    }

                }
            }
        }
        return s.substr(maxEnd - maxLen+1, maxLen);
    }
};

这给我们提供了一个复杂度为 $O(n^2)$ 动态规划解法,它将占用 $O(n)$ 的空间。

方法二:暴力法

很明显,暴力法将选出所有子字符串可能的开始和结束位置,并检验它是不是回文。

复杂度分析

时间复杂度: $O(n^3)$ ,假设n是输入字符串的长度,则 $\binom{n}{2} = \frac{n(n-1)}{2}$ ,为此类子字符串(不包括字符本身是回文的一般解法)的总数。因为验证每个子字符串需要 $O(n)$ 的时间,所以运行时间复杂度是 $O(n^3)$ 。

空间复杂度: $O(1)$ 。

class Solution {
    public:
        string longestPalindrome(string s) {
            string ans;
            int max_value=0,len=s.length();
            for(int i=0;i<len;i++)
                for(int j=i+1;j<=len;j++){
                    string test=s.substr(i,j-i);
                    if(isPalindromic(test) && test.length() > max_value){
                        ans=s.substr(i,j-i);
                        max_value=max(max_value,int(ans.length()));
                    }
                }
            return ans;
        }
        bool isPalindromic(string s){
            int len = s.length();
            for(int i =0;i<len/2;i++){
                if(s[i] != s[len-i-1]){
                    return false;
                }
            }
            return true;
        }
};

方法三:动态规划

为了改进暴力法,我们首先观察如何避免在验证回文时进行不必要的重复计算。考虑"ababa"这个示例。如果我们已经知道"bab"是回文,那么很明显,"ababa"一定是回文,因为它的左首字母和右尾字母是相同的。

我们给出 $P(i,j)$ 的定义如下:

$P(i,j) = \begin{cases} \text{true,} &\quad\text{如果子串} S_i \dots S_j \text{是回文子串}\\ \text{false,} &\quad\text{其它情况} \end{cases}$

因此,

$P(i, j) = ( P(i+1, j-1) \text{ and } S_i == S_j )$

基本示例如下:

$\begin{aligned} & P(i,i)=true \\ & P(i, i+1) = ( S_i == S_{i+1} ) \end{aligned}$

这产生了一个直观的动态规划解法,我们首先初始化一字母和二字母的回文,然后找到所有三字母回文,并依此类推…

class Solution {
    public:
        string longestPalindrome(string s) {
            int len = s.length();
            string res;
            vector<bool> P;
            for(int i=0;i<len;i++) P.push_back(false);
            for(int i=len-1;i>=0;i--)
                for(int j=len-1;j>=i;j--){
                    P[j] = s[i]==s[j] && (j-i<3||P[j-1]);
                    if (P[j] && j - i + 1 > res.length()) {
                        res = s.substr(i, j + 1-i);
                    }
                }
            return res;
        }  
};

复杂度分析

时间复杂度: $O(n^2)$ ,这里给出我们的运行时间复杂度为 $O(n^2)$ 。

空间复杂度: $O(n^2)$ ,该方法使用 $O(n^2)$ 的空间来存储表。

方法四:中心扩展算法

事实上,只需使用恒定的空间,我们就可以在 $O(n^2)$ 的时间内解决这个问题。我们观察到回文中心的两侧互为镜像。因此,回文可以从它的中心展开,并且只有 $2n - 1$ 个这样的中心。你可能会问,为什么会是 $2n - 1$ 个,而不是n个中心?原因在于所含字母数为偶数的回文的中心可以处于两字母之间(例如"abba"的中心在两个'b'之间)。

class Solution {
    public:
        string longestPalindrome(string s) {
            if (s == "" || s.length() < 1) return "";
            int start = 0, end = 0;
            for (int i = 0; i < s.length(); i++) {
                int len1 = expandAroundCenter(s, i, i);
                int len2 = expandAroundCenter(s, i, i + 1);
                int len = max(len1, len2);
                if (len > end - start) {
                    start = i - (len - 1) / 2;
                    end = i + len / 2;
                }
            }
            return s.substr(start, end + 1-start);  
        }
        int expandAroundCenter(string s,int left, int right){
            int L=left,R=right;
            while(L>=0 && R<s.length() &&s[L]==s[R]){
                L--,R++;
            }
            return R-L-1;
        }
};

复杂度分析

时间复杂度: $O(n^2)$ ,由于围绕中心来扩展回文会耗去 $O(n)$ 的时间,所以总的复杂度为 $O(n^2)$ 。

空间复杂度: $O(1)$ 。

方法五:Manacher算法

还有一个复杂度为 $O(n)$ 的Manacher算法。然而,这是一个非同寻常的算法,在45分钟的编码时间内提出这个算法将会是一个不折不扣的挑战。理解它,我保证这将是非常有趣的。

马拉车算法Manacher‘s Algorithm是用来查找一个字符串的最长回文子串的线性方法,由一个叫Manacher的人在1975年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。

首先我们解决下奇数和偶数的问题,在每个字符间插入"#",并且为了使得扩展的过程中,到边界后自动结束,在两端分别插入"^"和 "$",两个不可能在字符串中出现的字符,这样中心扩展的时候,判断两端字符是否相等的时候,如果到了边界就一定会不相等,从而出了循环。经过处理,字符串的长度永远都是奇数了。

首先我们用一个数组P保存从中心扩展的最大个数,而它刚好也是去掉"#"的原字符串的总长度。例如下图中下标是6的地方,可以看到P[6]等于5,所以它是从左边扩展5个字符,相应的右边也是扩展5个字符,也就是"#c#b#c#b#c#"。而去掉#恢复到原来的字符串,变成"cbcbc",它的长度刚好也就是5。

求原字符串下标

用P的下标i减去P[i],再除以2,就是原字符串的开头下标了。

例如我们找到P[i]的最大值为5,也就是回文串的最大长度是5,对应的下标是6,所以原字符串的开头下标是(6-5)/2= 0。所以我们只需要返回原字符串的第0到第(5-1)位就可以了。

求每个P[i]

接下来是算法的关键了,它充分利用了回文串的对称性。

我们用C表示回文串的中心,用R表示回文串的右边半径。所以R=C+P[i]。C和R所对应的回文串是当前循环中R最靠右的回文串。

让我们考虑求P[i]的时候,如下图。用i_mirror表示当前需要求的第i个字符关于C对应的下标。

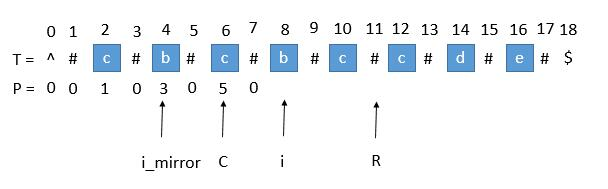
我们现在要求P[i],如果是用中心扩展法,那就向两边扩展比对就行了。但是我们其实可以利用回文串C的对称性。i 关于C的对称点是i_mirror,P[i_mirror]=3,所以P[i]也等于3。

但是有三种情况将会造成直接赋值为P[i_mirror]是不正确的,下边一一讨论。

超出了R

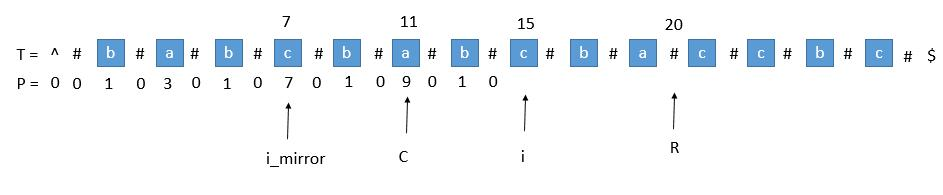
当我们要求P[i]的时候,P[mirror]=7,而此时P[i]并不等于7,为什么呢,因为我们从i开始往后数7个,等于22,已经超过了最右的R,此时不能利用对称性了,但我们一定可以扩展到R的,所以P[i]至少等于R-i= 20-15=5,会不会更大呢,我们只需要比较T[R+1] 和T[R+1]关于i的对称点就行了,就像中心扩展法一样一个个扩展。

P[i_mirror]遇到了原字符串的左边界

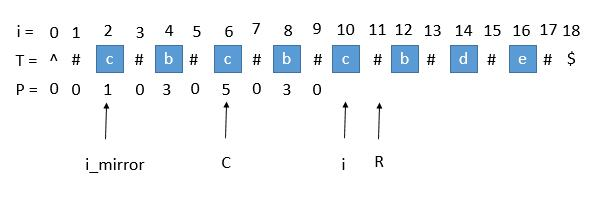
此时P[i_mirror]=1,但是P[i]赋值成1是不正确的,出现这种情况的原因是P[i_mirror]在扩展的时候首先是"#"=="#",之后遇到了"^"和另一个字符比较,也就是到了边界,才终止循环的。而P[i]并没有遇到边界,所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。

i等于了R

此时我们先把P[i]赋值为0,然后通过中心扩展法一步一步扩展就行了。

考虑C和R的更新

就这样一步一步的求出每个P[i],当求出的P[i]的右边界大于当前的R时,我们就需要更新C和R为当前的回文串了。因为我们必须保证i在R里面,所以一旦有更右边的R就要更新R。

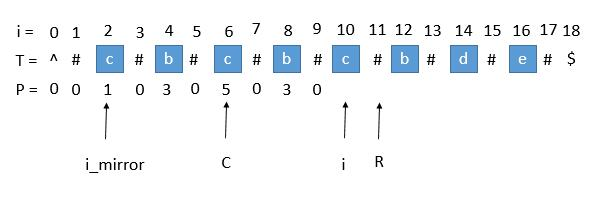
此时的P[i]求出来将会是3,P[i]对应的右边界将是10+3=13,所以大于当前的R,我们需要把C更新成i的值,也就是10,R更新成13。继续下边的循环。

class Solution {
    public:
        // 马拉车算法
        string longestPalindrome(string s) {
            string T = preProcess(s);
            int n = T.length();
            vector<int> P;
            for(int i=0;i<n;i++) P.push_back(0);
            int C = 0, R = 0;

            for (int i = 1; i < n - 1; i++) {
                int i_mirror = 2 * C - i;
                if (R > i) P[i] = min(R - i, P[i_mirror]);// 防止超出 R
                else P[i]=0; // 等于 R 的情况


                // 碰到之前讲的三种情况时候，需要利用中心扩展法
                while (T[i+1+P[i]] == T[i-1-P[i]]) P[i]++;

                // 判断是否需要更新 R
                if (i + P[i] > R) C = i, R = i + P[i];
            }

            // 找出 P 的最大值
            int maxLen = 0, centerIndex = 0;
            for(int i = 1; i < n - 1; i++) 
                if (P[i] > maxLen) 
                    maxLen = P[i], centerIndex = i;

            int start = (centerIndex - maxLen) / 2; //最开始讲的求原字符串下标
            return s.substr(start, maxLen);
        }

        string preProcess(string s){
            int n=s.length();
            if(n==0) return "^$";
            string ret="^";
            for(int i=0;i<n;i++)
                ret = ret + "#" + s[i];
            ret = ret + "#$";
            return ret;
        }
};

复杂度分析:

时间复杂度:for循环里边套了一层while循环,难道不是 $O(n^2)$ ?不!其实是 $O(n)$ 。不严谨的想一下,因为while循环访问R右边的数字用来扩展,也就是那些还未求出的节点,然后不断扩展,而期间访问的节点下次就不会再进入while了,可以利用对称得到自己的解,所以每个节点访问都是常数次,所以是 $O(n)$ 。

空间复杂度: $O(n)$ 。