音频知识

一、基本参数

人耳可以听到的声音频率在20HZ~20kHz之间的声波,称为音频。

1.1 基本概念

1.1.1 采样率**

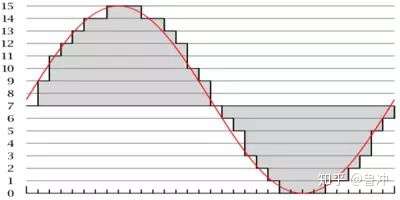
数码音频系统是通过将声波波形转换成一连串的二进制数据来再现原始声音的(原始声音是模拟信号),实现这个步骤使用的设备是模/数转换器(A/D转换器,或者ADC,或者analog to digital convert)。它以每秒上万次的速率对声波进行采样,每一次采样都记录下了原始模拟声波在某一时刻的状态,称之为样本。将一串的样本连接起来,就可以描述一段声波了,把每一秒钟所采样的数目称为采样频率或采样率,单位为Hz(赫兹)。采样频率越高所能描述的声波频率就越高。采样率决定声音频率的范围(相当于音调),可以用数字波形表示。以波形表示的频率范围通常被称为带宽。在当今的主流采集卡上,采样频率一般共分为22.05KHz、44.1KHz(44100Hz)、48KHz三个等级,22.05 KHz只能达到FM广播的声音品质,44.1KHz则是理论上的CD音质界限,48KHz则更加精确一些。对于高于48KHz的采样频率人耳已无法辨别出来了,所以在电脑上没有多少使用价值。

5kHz的采样率仅能达到人们讲话的声音质量。

11kHz的采样率是播放小段声音的最低标准,是CD音质的四分之一。

22kHz采样率的声音可以达到CD音质的一半,目前大多数网站都选用这样的采样率。

44kHz的采样率是标准的CD音质,可以达到很好的听觉效果。

Nyquist采样定理:只要采样频率大于被采样信号最高频率的两倍,就能完全恢复

采样率根据使用类型不同,大概有以下几种:

8kHz:电话等使用,对于记录人声足够使用,iphone的录音时,这个频率就够了

22.05kHz:广播使用频率

44.1kHz:音频CD

48kHz:DVD、数字电视中使用

96kHz-192kHz:DVD-Audio、蓝光高清等使用

1.1.2 采样位数(采样精度、量化格式)

电脑中的声音文件是用数字0和1来表示的。所以在电脑上录音的本质就是把模拟声音信号转换成数字信号。反之,在播放时则是把数字信号还原成模拟声音信号输出。采样位数可以理解为采集卡处理声音的解析度。这个数值越大,解析度就越高,录制和回放的声音就越真实。采集卡的位是指采集卡在采集和播放声音文件时所使用数字声音信号的二进制位数。采集卡的位客观地反映了数字声音信号对输入声音信号描述的准确程度。

1字节(也就是8bit)只能记录256个数,也就是只能将振幅划分成256个等级;

2字节(也就是16bit)可以细到65536个数,这已是CD标准了;

4字节(也就是32bit)能把振幅细分到4294967296个等级,实在是没必要了

1.1.3 动态范围

人耳可以感受到大约120dB的动态范围,其中0dB是不可察觉的,120dB是达到疼痛的阈值,虽然我们生活的动态范围,大部分处于更窄的范围中。在声音作品中,峰值电平和平均电平之间的范围,就是动态范围。如今流行音乐动态范围可能只有大约8-10dB,而电影可能有大约20dB动态范围,这也是为什么你会被电影院中爆炸声吓的从座位上跳起来,而不是在车里听一首歌的时候。

根据理论计算可以得知:1bit深度的动态范围的增量是6dB,比如一个比特深度(bit depth)为16bit的音频,无论他是wave还是aiff,这个音频文件的理论动态范围为16*6=96(dB),如果是24bit的话,其动态范围则为24*6=144(dB)。

1.1.4 比特率(bit rate)

其实是音频文件在被编码后,传输过程中的速率(传输速度),在视频工作者里所谓的对应音频的"码率",单位是bps(每秒内传输bit的数量)。在数字音频中,音频播放时的传输速率(比特率)对音质也会产生影响。

可能很多音频程序员很理解这里的原理,而对于大多数音乐人或录音师来说,并不会关注太多,主要原因是这和制作过程没太大关系,但问题往往都会发生在成品产出后,不同领域工作者对文件格式要求的问题,最后的结果是一旦有个文件在听感上出现了瑕疵(比如爆音,或动态不够),在排查问题的时候会耽误很多时间,甚至会造成误会。

Bit rate定义:比特率,每秒钟传输bit的量,单位为bps(bit per second),比特率越高,传输数据的速度越快,会间接影响音频的音质

1.1.5 通道数

即声音的通道的数目。常有单声道和立体声之分,单声道的声音只能使用一个喇叭发声(有的也处理成两个喇叭输出同一个声道的声音),立体声可以使两个喇叭都发声(一般左右声道有分工) ,更能感受到空间效果,当然还有更多的通道数。

1.1.6 VBR,ABR,CBR

VBR(Variable Bitrate)动态比特率。也就是没有固定的比特率,压缩软件在压缩时根据音频数据即时确定使用什么比特率。这是Xing发展的算法,他们将一首歌的复杂部分用高Bitrate编码,简单部分用低Bitrate编码。主意虽然不错,可惜Xing编码器的VBR算法很差,音质与CBR相去甚远。幸运的是,Lame完美地优化了VBR算法,使之成为MP3的最佳编码模式。这是以质量为前提兼顾文件大小的方式时推荐的编码模式。

ABR(Average Bitrate)平均比特率,是VBR的一种插值参数。Lame针对CBR不佳的文件体积比和VBR生成文件大小不定的特点独创了这种编码模式。ABR也被称为“Safe VBR”,它是在指定的平均Bitrate内,以每50帧(30帧约1秒)为一段,低频和不敏感频率使用相对低的流量,高频和大动态表现时使用高流量。举例来说,当指定用192kbps ABR对一段wav文件进行编码时,Lame会将该文件的85%用192kbps固定编码,然后对剩余15%进行动态优化:复杂部分用高于192kbps来编码、简单部分用低于192kbps来编码。与192kbps CBR相比,192kbps ABR在文件大小上相差不多,音质却提高不少。ABR编码在速度上是VBR编码的2到3倍,在128-256kbps范围内质量要好于CBR。可以做为VBR和CBR的一种折衷选择。

CBR(Constant Bitrate),常数比特率,指文件从头到尾都是一种位速率。相对于VBR和ABR来讲,它压缩出来的文件体积很大,但音质却不会有明显的提高。　　

1.1.7 有损和无损

根据采样和量化的过程可知,音频编码最多只能做到无限接近自然界的信号,至少目前的技术还不可能将其完全一样。这是因为自然界的信号是连续的,而音频编码后的值是离散的。因此,任何数字音频编码方案都是有损的,这也就意味着任何的音频都不可能完全还原出自然界的声音。

在计算机应用中, PCM编码能够达到最高保真水平。它已经被广泛地应用于素材保存及音乐欣赏,包括CD、DVD以及WAV文件等等。因此,PCM约定俗成了无损编码,但是这并不意味着PCM就能够确保信号绝对保真,PCM也只能做到最大程度的无限接近。习惯性地把MP3列入有损音频编码范畴,这是相对PCM编码的。

强调编码的相对性的有损和无损,要做到真正的无损是非常困难,甚至是不可能的。就如同,我们用小数去表达圆周率,不管小数精度有多高,也只能无限地接近,而不是真正等于圆周率的值。　　

1.1.8 其他参数

帧:帧记录了一个声音单元,其长度为样本长度(采样位数)和通道数的乘积

周期:音频设备一次处理所需要的帧数,对于音频设备的数据访问以及音频数据的存储,都是以此为单位。

交错模式:数字音频信号存储的方式。数据以连续帧的方式存放,即首先记录帧1的左声道样本和右声道样本,再开始帧2的记录...

非交错模式:首先记录的是一个周期内所有帧的左声道样本,再记录所有右声道样本。

1.2 文件组成

介绍

音频文件的组成:文件格式(或者音频容器)+数据格式(或者音频编码)。文件格式(或音频容器)是用于形容文件本身的格式。可以通过多种不同的方法为真正的音频数据编码。例如CAF文件便是一种文件格式,它能够包含MP3格式,线性PCM以及其它数据格式的音频。

数据格式(或音频编码):将从音频编码开始阐述(而不是文件格式),因为编码是最重要的环节。

线性PCM

这是表示线性脉冲编码调制,主要是描写用于将模拟声音数据转换成数字格式的技术。简单地说也就是未压缩的数据。因为数据是未压缩的,所以我们便可以最快速地播放出音频,而如果空间不是问题的话这便是iPhone音频的优先代码选择。

声音数据量的计算公式为:数据量(字节/秒)=(采样频率(Hz)×采样位数(bit)×声道数)/8(单声道的声道数为1,立体声的声道数为2)

WAVE

这是一种古老的音频文件格式,由微软开发。WAV是一种文件格式,符合 PIFF Resource Interchange FileFormat规范。所有的WAV都有一个文件头,这个文件头音频流的编码参数。WAV对音频流的编码没有硬性规定,除了PCM之外,还有几乎所有支持ACM规范的编码都可以为WAV的音频流进行编码。很多朋友没有这个概念,我们拿AVI做个示范,因为AVI和WAV在文件结构上是非常相似的,不过 AVI多了一个视频流而已。我们接触到的AVI有很多种,因此我们经常需要安装一些Decode才能观看一些AVI,我们接触到比较多的DivX就是一种视频编码,AVI可以采用DivX编码来压缩视频流,当然也可以使用其他的编码压缩。同样,WAV也可以使用多种音频编码来压缩其音频流,不过我们常见的都是音频流被PCM编码处理的WAV,但这不表示WAV只能使用PCM编码,MP3编码同样也可以运用在WAV中,和AVI一样,只要安装好了相应的 Decode,就可以欣赏这些WAV了。

MP3编码

MP3发展已经有10个年头了,他是MPEG(MPEG:Moving Picture Experts Group) AudioLayer-3的简称,是MPEG1的衍生编码方案,1993年由德国FraunhoferIIS研究院和汤姆生公司合作发展成功。MP3可以做到12:1的惊人压缩比并保持基本可听的音质,在当年硬盘天价的日子里,MP3迅速被用户接受,随着网络的普及,MP3被数以亿计的用户接受。MP3编码技术的发布之初其实是非常不完善的,由于缺乏对声音和人耳听觉的研究,早期的mp3编码器几乎全是以粗暴方式来编码,音质破坏严重。随着新技术的不断导入,mp3编码技术一次一次的被改良,其中有2次重大技术上的改进。

VBR:MP3格式的文件有一个有意思的特征,就是可以边读边放,这也符合流媒体的最基本特征。也就是说播放器可以不用预读文件的全部内容就可以播放,读到哪里播放到哪里,即使是文件有部分损坏。虽然mp3可以有文件头,但对于 mp3格式的文件却不是很重要,正因为这种特性,决定了MP3文件的每一段每一帧都可以单独的平均数据速率,而无需特别的解码方案。于是出现了一种叫 VBR(Variablebitrate,动态数据速率)的技术,可以让MP3文件的每一段甚至每一帧都可以有单独的bitrate,这样做的好处就是在保证音质的前提下最大程度的限制了文件的大小。这种技术的优越性是显而易见的,但要运用确实是一件难事,因为这要求编码器知道如何为每一段分配 bitrate,这对没有波形分析的编码器而言,这种技术如同虚设。正是如此,VBR技术并没有一出现就显得光彩夺目。

专家们通过长期的声学研究,发现人耳存在遮蔽效应。声音信号实际是一种能量波,在空气或其他媒介中传播,人耳对声音能量的多少即响度或声压最直接的反应就是听到这个声音的大小,我们称它为响度,表示响度这种能量的单位为分贝(dB)。即使是同样响度的声音,人们也会因为它们频率不同而感觉到声音大小不同。人耳最容易听到的就是4000Hz的频率,不管频率是否增高或降低,即使是响度在相同的情况下,大家都会觉得声音在变小。但响度降到一定程度时,人耳就听不到了,每一个频率都有着不同的值。

可以看到这条曲线基本成一个V字型,当频率超过15000Hz时,人耳的会感觉到声音很小,很多听觉不是很好的人,根本就听不到20000Hz的频率,不管响度有多大。当人耳同时听到两个不同频率、不同响度的声音时,响度较小的那个也会被忽略,例如:在白天我们很难听到电脑中散热风扇的声音,晚上却成了噪声源,根据这种原理,编码器可以过滤掉很多听不到的声音,以简化信息复杂度,增加压缩比,而不明显的降低音质。这种遮蔽被称为同时遮蔽效应。但声音 A被声音B遮蔽,如果A处于B为中心的遮蔽范围内,遮蔽会更明显,这个范围叫临界带宽。每一种频率的临界带宽都不一样,频率越高的临界带宽越宽。

据这种效应,专家们设计出人耳听觉心理模型,这个模型被导入到mp3编码中后,导致了一场翻天覆地的音质革命,mp3编码技术一直背负着音质差的恶名,但这个恶名现在已经逐渐被洗脱。到了此时,一直被埋没的VBR技术光彩四射,配合心理模型的运用便现实出强大的诱惑力与杀伤力。

二、传统特征

参考: https://www.cnblogs.com/xingshansi/p/6815217.html

2.1 过零率

过零率的表达式为:

$Z_n=\frac{1}{2}\sum_{m=0}^{N-1}|sgn[x_n(m)]-sgn[x_n(m-1)]|$

其中, $sgnn[]$ 是符号函数,其中 $N$ 为一帧的长度,n为对应的帧数,按帧处理。

过零率体现的是信号过零点的次数,体现的是频率特性。因为需要过零点,所以信号处理之前需要中心化处理。

过零率代码:

import math
import wave
import numpy as np
import pylab as pl

def ZeroCR(waveData, frameSize, overLap):
    wlen = len(waveData)
    step = frameSize - overLap
    frameNum = math.ceil(wlen/step)
    zcr = np.zeros((frameNum,1))
    for i in range(frameNum):
        curFrame = waveData[np.arange(i*step,min(i*step+frameSize,wlen))]
        curFrame = curFrame - np.mean(curFrame) # zero-justified
        zcr[i] = sum(curFrame[0:-1]*curFrame[1::]<=0)
    return zcr

# ============ test the algorithm =============
# read wave file and get parameters
filename = "./aeiou.wav"
fw = wave.open(filename,'rb')
params = fw.getparams()
print(params)
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = fw.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data.shape = -1, 1
fw.close()

# calculate Zero Cross Rate
frameSize = 256
overLap = 0
zcr = ZeroCR(wave_data, frameSize, overLap)

# plot the wave
time = np.arange(0, len(wave_data)) * (1.0 / framerate)
time2 = np.arange(0, len(zcr)) * (len(wave_data)/len(zcr) / framerate)
pl.subplot(211)
pl.plot(time, wave_data)
pl.ylabel("Amplitude")
pl.subplot(212)
pl.plot(time2, zcr)
pl.ylabel("ZCR")
pl.xlabel("time (seconds)")

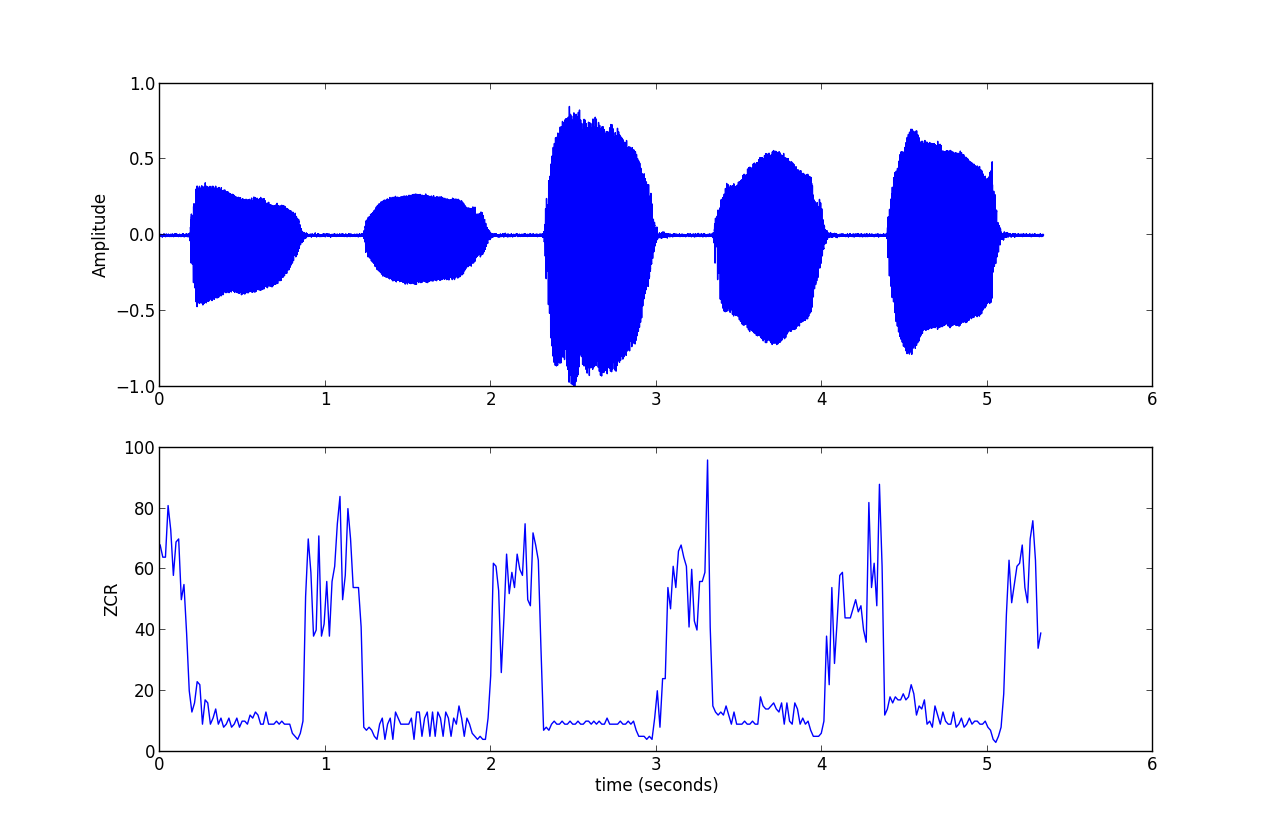
2.2 短时能量

短时能量的表达式为:

$E_n=\sum_{m=0}^{N-1}x_n^2(m)$

其中 $N$ 为信号帧长,短时能量体现的是信号在不同时刻的强弱程度。

import math
import wave
import numpy as np

# 计算每一帧的能量256个采样点为一帧
def calEnergy(wave_data) :
    energy = []
    sum = 0
    for i in range(len(wave_data)) :
        sum = sum + (int(wave_data[i]) * int(wave_data[i]))
        if (i + 1) % 256 == 0 :
            energy.append(sum)
            sum = 0
        elif i == len(wave_data) - 1 :
            energy.append(sum)
    return energy

filename = "./aeiou.wav"
fw = wave.open(filename,'rb')
params = fw.getparams()
# nframes采样点数目
nchannels, sampwidth, framerate, nframes = params[:4]
# readframes()按照采样点读取数据
str_data = f.readframes(nframes)            # str_data 是二进制字符串

# 转成二字节数组形式(每个采样点占两个字节）
wave_data = np.fromstring(str_data, dtype = np.short)
print( "采样点数目:" + str(len(wave_data)))          #输出应为采样点数目
f.close()
energy = calEnergy(wave_data)
print("能量为:{}".format(energy))

2.3 短时自相关函数

短时自相关函数定义式为:

理论分析:学过信号处理的都应该知道,信号A与信号B翻转的卷积,就是二者的相关函数。其中是因为分帧的时候,加了窗函数截断,w代表窗函数。

2.4 短时平均幅度差

假设x是加窗截断后的信号,短时平均幅度差定义:

理论分析:音频具有周期特性,平稳噪声情况下利用短时平均幅度差可以更好地观察周期特性。

2.5 语谱图(基于FFT)

有时FFT也换成DCT实现,FFT延展与DCT是等价的,就不一一列出了。只分析FFT情况。

基于FFT语谱图的定义:

就是分帧,对每一帧信号FFT

然后求绝对值/平方。

理论分析:

给出示意图,语音分帧→每一帧分别FFT→求取FFT之后的幅度/能量,这些数值都是正值,类似图像的像素点,显示出来就是语谱图。

2.6 短时功率谱密度

先来看看功率谱定义:

可见对于有限的信号,功率谱之所以可以估计,是基于两点假设:1)信号平稳; 2)随机信号具有遍历性

2.7 谱熵

谱熵的定义,首先对每一帧信号的频谱绝对值归一化:

这样就得到了概率密度,进而求取熵:

理论分析:熵体现的是不确定性,例如抛骰子一无所知,每一面的概率都是1/6,信息量最大,也就是熵最大。如果知道商家做了手脚,抛出3的概率大,这个时候我们已经有一定的信息量,抛骰子本身的信息量就少了,熵也就变小。对于信号,如果是白噪声,频谱类似均匀分布,熵就大一些;如果是语音信号,分布不均匀,熵就小一些,利用这个性质也可以得到一个粗糙的VAD(有话帧检测)。谱熵有许多的改进思路,滤波取特定频段、设定概率密度上限、子带平滑谱熵,自带平滑通常利用拉格朗日平滑因子,这是因为防止某一段子带没有信号,这个时候的概率密度就没有意义了,这个思路在利用统计信息估计概率密度时经常用到,比如朴素贝叶斯就用到这个思路。

2.8 基频

基频:也就是基频周期。人在发音时,声带振动产生浊音(voiced),没有声带振动产生清音(Unvoiced)。浊音的发音过程是:来自肺部的气流冲击声门,造成声门的一张一合,形成一系列准周期的气流脉冲,经过声道(含口腔、鼻腔)的谐振及唇齿的辐射形成最终的语音信号。故浊音波形呈现一定的准周期性。所谓基音周期,就是对这种准周期而言的,它反映了声门相邻两次开闭之间的时间间隔或开闭的频率。常用的发声模型:

基音提取常用的方法有:倒谱法、短时自相关法、短时平均幅度差法、LPC法,这里借用上面的短时自相关法,说一说基频提取思路。

自相关函数:

通常进行归一化处理,因为r(0)最大,

得到归一化相关函数时候,归一化的相关函数第一个峰值为k = 0,第二个峰值理论上应该对应基频的位置,因为自相关函数对称,通常取一半分析即可。

取一帧信号为例,整个说话段要配合有话帧检测(VAD技术,这里不提了)自相关法估计基频code:

卷积还是调用上面的函数。波形的短时周期还是比较明显的,给出一帧信号:

2.9 共振峰

首先给出共振峰定义:当声门处准周期脉冲激励进入声道时会引起共振特性,产生一组共振频率,这一组共振频率称为共振峰频率或简称共振峰。

共振峰参数包括共振峰频率和频带的宽度,它是区别不同韵母的重要参数,由于共振峰包含在语音的频谱包络中,因此共振峰参数的提取关键是估计自然语音的频谱包络,并认为谱包括的极大值就是共振峰,通常认为共振峰数量不超过4个。发声模型:

对这个模型抽象,通常有声管模型、声道模型两个思路,以声道模型为例:认为信号经过与声道的卷积,得到最终发出的声音。声道就是系统H。

共振峰的求解思路非常多,这里给出一个基于LPC内插的例子。

如果表达这个系统响应H呢？一个基本的思路就是利用全极点求取:

从按照时域里信号与声道卷积的思路,频域就是信号与声道相乘,所以声道就是包络:

利用线性预测系数(LPC)并选择适当阶数,可以得到声道模型H。LPC之前有分析过,可以点击这里。

其实利用LPC得出的包络,找到四个峰值,就已经完成了共振峰的估计。为了更精确地利用LPC求取共振峰有,两种常用思路:抛物线内插法、求根法,这里以内插法为例。其实就是一个插值的思路,如图

为了估计峰值,取p(k-1)、p(k)、p(k+1)哪一个点都是不合适的,插值构造抛物线,找出峰值就更精确了。

LPC内插法code:

2.10 mfcc特征

https://blog.csdn.net/zouxy09/article/details/9156785

梅尔倒谱系数(Mel-scale FrequencyCepstral Coefficients,简称MFCC)。依据人的听觉实验结果来分析语音的频谱,mfcc分析依据的听觉机理有两个:

第一Mel scale:人耳感知的声音频率和声音的实际频率并不是线性的,有下面公式

$f_{mel}=2595*\log_{10}(1+\frac{f}{100})$

$f=700(10^{f_{meel}}-1)$

式中 $f_{mel}$ 是以梅尔(Mel)为单位的感知频域(简称梅尔频域), $f$ 是以Hz为单位的实际语音频率。 $f_{mel}$ 与 $f$ 的关系曲线如下图所示,若能将语音信号的频域变换为感知频域中,能更好的模拟听觉过程的处理。

第二临界带(Critical Band):把进入人耳的声音频率用临界带进行划分,将语音在频域上就被划分成一系列的频率群,组成了滤波器组,即Mel滤波器组。

研究表明,人耳对不同频率的声波有不同的听觉敏感度。从200Hz到5000Hz的语音信号对语音的清晰度影响较大。两个响度不等的声音作用于人耳时,则响度较高的频率成分的存在会影响到对响度较低的频率成分的感受,使其变得不易察觉,这种现象称为掩蔽效应。

由于频率较低的声音(低音)在内耳蜗基底膜上行波传递距离大于频率较高的声音(高音),因此低音容易掩蔽高音。低音掩蔽的临界带宽较高频要小。所以,人们从低频到高频这一段频带内按临界带宽的大小由密到疏安排一组带通滤波器,对输入信号进行滤波。将每个带通滤波器输出的信号能量作为信号的基本特征,对此特征经过进一步处理后就可以作为语音的输入特征。由于这种特征不依赖于信号的性质,对输入信号不做任何的假设和限制,又利用了听觉模型的研究成果。因此,这种参数比基于声道模型的LPCC相比具有更好的鲁棒性,更符合人耳的听觉特性,而且当信噪比降低时仍然具有较好的识别性能。

求MFCC的步骤:

将信号帧化为短帧

对于每个帧,计算每帧语音的功率谱(周期图估计)

将mel滤波器组应用于功率谱,求滤波器组的能量,将每个滤波器中的能量相加

取所有滤波器组能量的对数

DCT变换

预处理

预处理包括预加重、分帧、加窗函数。假设我们的语音信号采样频率为8000Hz,语音数据在这里获取

import numpy
import scipy.io.wavfile
from scipy.fftpack import dct

sample_rate, signal = scipy.io.wavfile.read('OSR_us_000_0010_8k.wav') 
signal = signal[0:int(3.5 * sample_rate)]  # 这里只取前3.5s

预加重

预加重滤波器在以下几个方面很有用:

平衡频谱,因为高频通常与较低频率相比具有较小的幅度

避免在傅里叶变换操作期间的数值问题和

改善信号 -- 噪声比(SNR)

消除发声过程中声带和嘴唇的效应,来补偿语音信号受到发音系统所抑制的高频部分,也为了突出高频的共振峰。

预加重处理其实是将语音信号通过一个高通滤波器:

$y(t)-\alpha(t-1)$

其中滤波器系数( $\alpha$ )的通常为0.95或0.97,这里取pre_emphasis =0.97:

emphasized_signal = numpy.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])

分帧

在预加重之后,我们需要将信号分成短时帧。因此在大多数情况下,语音信号是非平稳的,对整个信号进行傅里叶变换是没有意义的,因为我们会随着时间的推移丢失信号的频率轮廓。语音信号是短时平稳信号。因此我们在短时帧上进行傅里叶变换,通过连接相邻帧来获得信号频率轮廓的良好近似。

将信号帧化为20-40ms帧。25毫秒是标准的frame_size=0.025。这意味着8kHz信号的帧长度为0.025*8000=200个采样点。帧移通常为10ms,即frame_stride=0.01(80个采样点),为了避免相邻两帧的变化过大,因此会让两相邻帧之间有一段重叠区域,此重叠区域包含了120个取样点,通常约为每帧语音的1/2或1/3。第一个语音帧0开始,下一个语音帧从160开始,直到到达语音文件的末尾。如果语音文件没有划分为偶数个帧，则用零填充它以使其完成。

frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate  # 从秒转换为采样点
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
# 确保我们至少有1帧
num_frames = int(numpy.ceil(float(numpy.abs(signal_length - frame_length)) / frame_step))  

pad_signal_length = num_frames * frame_step + frame_length
z = numpy.zeros((pad_signal_length - signal_length))
# 填充信号,确保所有帧的采样数相等,而不从原始信号中截断任何采样
pad_signal = numpy.append(emphasized_signal, z) 

indices = numpy.tile(numpy.arange(0, frame_length), (num_frames, 1)) + numpy.tile(numpy.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(numpy.int32, copy=False)]

加窗

将每一帧乘以汉明窗,以增加帧左端和右端的连续性。抵消fft假设的数据是无限的,并减少频谱泄漏。假设分帧后的信号为S(n),n=0,1,...,N-1,,N为窗口长度,那么乘上汉明窗

$S'(n)=S(n)\times W(n)$

后,汉明窗 $W(n)$ 形式如下:

$W(n,\alpha)=(1-\alpha)-\alpha\times \cos(\frac{2\pi n}{N-1}) ,0\le n \le N-1$

frames *= numpy.hamming(frame_length)
# frames *= 0.54 - 0.46 * numpy.cos((2 * numpy.pi * n) / (frame_length - 1))  # 内部实现

FFT

由于信号在时域上的变换通常很难看出信号的特性,所以通常将它转换为频域上的能量分布来观察,不同的能量分布,就能代表不同语音的特性。对分帧加窗后的各帧信号进行做一个N点FFT来计算频谱,也称为短时傅立叶变换(STFT),其中N通常为256或512,NFFT＝512:

$S_i(k)=\sum_{n=1}^Ns_i(n)e^{-j2\pi kn/N},1\le k\le K$

mag_frames = numpy.absolute(numpy.fft.rfft(frames, NFFT))   # fft的幅度

能量谱

计算功率谱(周期图),对语音信号的频谱取模平方(取对数或者去平方,因为频率不可能为负,负值要舍去)得到语音信号的谱线能量。

$P=\frac{|FFT(x_i)|^2}{N}$

其中, $X_i$ 是信号 $X$ 的第i帧,这可以用以下几行来实现：

pow_frames = ((1.0 / NFFT) * ((mag_frames) ** 2))  # 功率谱

使用Mel刻度滤波器组过滤

计算通过Mel滤波器,将功率谱通过一组Mel刻度(这里取40个)的三角滤波器组提取带宽。

这个Mel滤波器组就像人类的听觉感知系统(耳朵),人耳只关注某些特定的频率分量(人的听觉对频率是有选择性的)。它对不同频率信号的灵敏度是不同的,换言之,它只让某些频率的信号通过,而压根就直接无视它不想感知的某些频率信号。但是这些滤波器在频率坐标轴上却不是统一分布的,在低频区域有很多的滤波器,他们分布比较密集,但在高频区域,滤波器的数目就变得比较少,分布很稀疏。

定义一个有M个三角滤波器的滤波器组(滤波器的个数和临界带的个数相近),中心频率为 $f(m)$ ,中心频率响应为1,并且朝向0线性减小,直到它达到响应为0的两个相邻滤波器的中心频率,如下图所示。M通常取22-40,26是标准,本文取nfilt=40。各 $f(m)$ 之间的间隔随着m值的增大而增宽,如图所示:

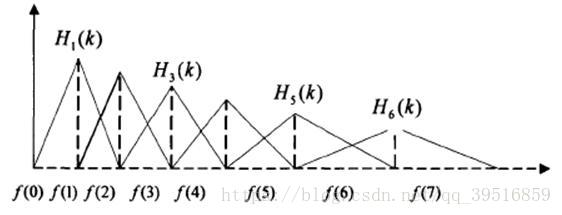
这可以通过以下等式建模,三角滤波器的频率响应定义为:

$H_m(k) = \begin{cases} \hfill 0 \hfill & k < f(m - 1) \\ \hfill \dfrac{k - f(m - 1)}{f(m) - f(m - 1)} \hfill & f(m - 1) \leq k < f(m) \\ \hfill 1 \hfill & k = f(m) \\ \hfill \dfrac{f(m + 1) - k}{f(m + 1) - f(m)} \hfill & f(m) < k \leq f(m + 1) \\ \hfill 0 \hfill & k > f(m + 1) \\ \end{cases}$

对于FFT得到的幅度谱,分别跟每一个滤波器进行频率相乘累加,得到的值即为该帧数据在在该滤波器对应频段的能量值。如果滤波器的个数为22,那么此时应该得到22个能量值

low_freq_mel = 0
high_freq_mel = (2595 * numpy.log10(1 + (sample_rate / 2) / 700))  # 将Hz转换为Mel
mel_points = numpy.linspace(low_freq_mel, high_freq_mel, nfilt + 2)  # 使得Mel scale间距相等
hz_points = (700 * (10**(mel_points / 2595) - 1))  # 将Mel转换为Hz
bin = numpy.floor((NFFT + 1) * hz_points / sample_rate)

fbank = numpy.zeros((nfilt, int(numpy.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
    f_m_minus = int(bin[m - 1])   # 左
    f_m = int(bin[m])             # 中
    f_m_plus = int(bin[m + 1])    # 右

    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
filter_banks = numpy.dot(pow_frames, fbank.T)
filter_banks = numpy.where(filter_banks == 0, numpy.finfo(float).eps, filter_banks)  # 数值稳定性
filter_banks = 20 * numpy.log10(filter_banks)  # dB

信号的功率谱经过滤波器组后,得到的谱图为:

如果经过Mel scale滤波器组得到的频谱是所需的特征,那么我们可以跳过均值归一化。

能量值取对数

由于人耳对声音的感知并不是线性的,用log这种非线性关系更好描述。取完log以后才可以进行倒谱分析。

$s\left( m \right)=\ln \left( {{\sum\limits_{K=0}^{N-1}{\left| {{X}_{a}}\left( k \right) \right|}}^{2}}{{H}_{m}}\left( k \right) \right),0\le m\le M$

离散余弦变换(DCT)

前一步骤中计算的滤波器组系数是高度相关的,这在一些机器学习算法中可能是有问题的。因此,我们可以应用离散余弦变换(DCT)去相关滤波器组系数并产生滤波器组的压缩表示。通常,对于自动语音识别(ASR),保留所得到的倒频谱系数2-13,其余部分被丢弃;num_ceps=12。丢弃其他系数的原因是它们代表滤波器组系数的快速变化,并且这些精细的细节对自动语音识别(ASR)没有贡献。

$C(n)=\sum\limits_{m=0}^{N-1}{s( m)\cos( \frac{\pi n( m-0.5)}{M} )},n=1,2,...,L$

L阶指MFCC系数阶数,通常取2-13。这里M是三角滤波器个数。

mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)] # 保持在2-13

可以将正弦提升器(Liftering在倒谱域中进行过滤。注意在谱图和倒谱图中分别使用filtering和liftering)应用于MFCC以去强调更高的MFCC,其已经声称可以改善噪声信号中的语音识别。

(nframes, ncoeff) = mfcc.shape
n = numpy.arange(ncoeff)
lift = 1 + (cep_lifter / 2) * numpy.sin(numpy.pi * n / cep_lifter)
mfcc *= lift

由此产生的MFCC:

均值归一化

如前所述,为了平衡频谱并改善信噪比(SNR),我们可以简单地从所有帧中减去每个系数的平均值。

filter_banks -= (numpy.mean(filter_banks, axis=0) + 1e-8)

均值归一化滤波器组:

同样对于MFCC:

mfcc -= (numpy.mean(mfcc, axis=0) + 1e-8)

均值归一化MFCC:

用librosa提取MFCC特征

MFCC特征是一种在自动语音识别和说话人识别中广泛使用的特征。在librosa中,提取MFCC特征只需要一个函数:

librosa.feature.mfcc(y=None, sr=22050, S=None, n_mfcc=20, dct_type=2, norm='ortho', **kwargs)

参数:

y:音频时间序列

sr:音频的采样率

S:np.ndarray,对数功率梅尔频谱,这个函数既可以支持时间序列输入也可以支持频谱输入,都是返回MFCC系数

n_mfcc:int>0,要返回的MFCC数,scale滤波器组的个数,通常取22~40,本文取40

dct_type:None,or {1, 2, 3},离散余弦变换(DCT)类型。默认情况下,使用DCT类型2

norm:None or 'ortho'规范。如果dct_type为2或3,则设置norm ='ortho'使用正交DCT基础。norm不支持dct_type=1

M:np.ndarray MFCC序列

import librosa

y, sr = librosa.load('./train_nb.wav', sr=16000)
# 提取 MFCC feature
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)

print(mfccs.shape)        # (40, 65)

三、librosa库

参考文档: http://librosa.github.io/librosa/core.html

读取音频

>>> import librosa
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav')
>>> y
array([  0.00000000e+00,   0.00000000e+00,   0.00000000e+00, ...,
         8.12290182e-06,   1.34394732e-05,   0.00000000e+00], dtype=float32)
>>> sr
22050

librosa默认的采样率是22050,如果需要读取原始采样率,需要设定参数sr=None:

>>> import librosa
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> sr
44100

可见,'beat.wav'的原始采样率为44100。如果需要重采样,只需要将采样率参数sr设定为你需要的值:

>>> import librosa
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=16000)
>>> sr
16000

提取Log-Mel Spectrogram特征

Log-Mel Spectrogram特征是目前在语音识别和环境声音识别中很常用的一个特征,由于CNN在处理图像上展现了强大的能力,使得音频信号的频谱图特征的使用愈加广泛,甚至比MFCC使用的更多。

>>> import librosa
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> # extract mel spectrogram feature
>>> melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, hop_length=512, n_mels=128)
>>> # convert to log scale
>>> logmelspec = librosa.power_to_db(melspec)
>>> logmelspec.shape
(128, 194)

可见,Log-Mel Spectrogram特征是二维数组的形式,128表示Mel频率的维度(频域),194为时间帧长度(时域),所以Log-Mel Spectrogram特征是音频信号的时频表示特征。其中n_fft指的是窗的大小,这里为1024;hop_length表示相邻窗之间的距离,这里为512,也就是相邻窗之间有50%的overlap;n_mels为mel bands的数量,这里设为128。

提取MFCC特征

MFCC特征是一种在自动语音识别和说话人识别中广泛使用的特征。

>>> import librosa
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> # extract mfcc feature
>>> mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)
>>> mfccs.shape
(40, 194)

绘制声音波形

librosa有显示声音波形函数waveplot():

>>> import librosa
>>> import librosa.display
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> # plot a wavform
>>> plt.figure()
>>> librosa.display.waveplot(y, sr)
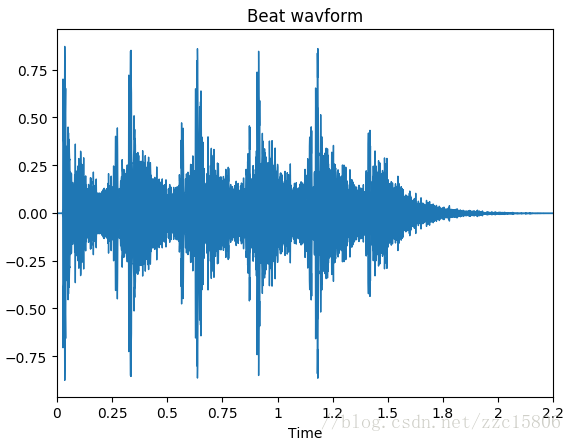
>>> plt.title('Beat wavform')
>>> plt.show()

输出图形为:

绘制频谱图

librosa有显示频谱图波形函数specshow():

>>> import librosa
>>> import librosa.display
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> # extract mel spectrogram feature
>>> melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, hop_length=512, n_mels=128)
>>> # convert to log scale
>>> logmelspec = librosa.power_to_db(melspec)
>>> # plot mel spectrogram
>>> plt.figure()
>>> librosa.display.specshow(logmelspec, sr=sr, x_axis='time', y_axis='mel')
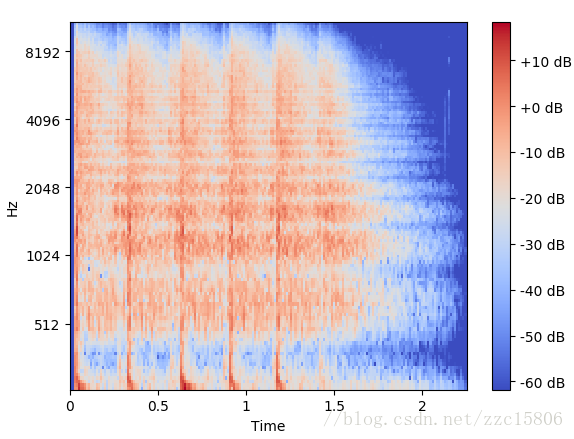
>>> plt.title('Beat wavform')
>>> plt.show()

输出结果为:

将声音波形和频谱图绘制在一张图表中:

>>> import librosa
>>> import librosa.display
>>> # Load a wav file
>>> y, sr = librosa.load('./beat.wav', sr=None)
>>> # extract mel spectrogram feature
>>> melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, hop_length=512, n_mels=128)
>>> # convert to log scale
>>> logmelspec = librosa.power_to_db(melspec)
>>> plt.figure()
>>> # plot a wavform
>>> plt.subplot(2, 1, 1)
>>> librosa.display.waveplot(y, sr)
>>> plt.title('Beat wavform')
>>> # plot mel spectrogram
>>> plt.subplot(2, 1, 2)
>>> librosa.display.specshow(logmelspec, sr=sr, x_axis='time', y_axis='mel')
>>> plt.title('Mel spectrogram')
>>> plt.tight_layout() #保证图不重叠
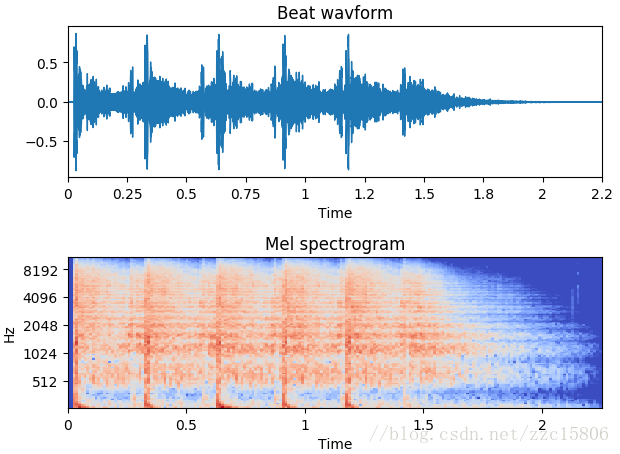
>>> plt.show()

输出结果为: